- Gerar link
- X
- Outros aplicativos
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.
ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.
NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.
JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.
TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :
sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
sistema indeterminístico Graceli ;
SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +
SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos
SISTEMA GRACELI INFINITO-DIMENSIONAL.
SISTEMA GRACELI INFINITO-DIMENSIONAL.
COM ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.
ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.
TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO E ESPECÍFICO NÍVEL DE ENERGIA.
SISTEMA MULTIDIMENSIONAL GRACELI
ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.
Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].
Quando um líquido composto por dois ou mais componentes é aquecido, o ponto de bolha é a temperatura (a uma dada pressão) onde a primeira bolha de vapor é formada. Dado que o vapor, provavelmente, terá uma composição diferente do líquido o ponto de bolha (junto com o ponto de orvalho) em diferentes composições são dados úteis no projeto de sistemas de destilação (como em refinarias de petróleo).
Para um único componente, o ponto de bolha e o ponto de orvalho são os mesmos e são referidos como o ponto de ebulição.
Calculando o ponto de bolha
Em um ponto de bolha, as seguintes relações mantem-se:
- ////
TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :
sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
onde
.
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
K é o coeficiante de distribuição ou fator K, definido como a razão da fração molar na fase de vapor 

Quando a lei de Raoult e lei de Dalton sustentam-se para a mistura, o fator K é definido como a razão entre a pressão de vapor à pressão total do sistema:[1]
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
Proposta pelo físico estadunidense Josiah Willard Gibbs, a Regra das Fases de Gibbs apresenta um critério para a determinação das fases que coexistirão em um sistema em equilíbrio num diagrama de fase.[1]
Definição
A regra das fases de Gibbs é expressa pela equação
,
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
em que P é o número de fases presentes, F é o número de graus de liberdade, ou o número de variáveis que podem ser controladas externamente, e que devem ser especificadas para definir por completo o estado de um sistema. O parâmetro C representa o número de componentes e N é o número de variáveis não relacionadas à composição. Como muitas vezes essas variáveis são a temperatura e a pressão, é comum a equação aparecer como:
.
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
Sistema unário
Para sistemas com um só componente, em que C = 1 e as variáveis são temperatura e pressão, de modo que N = 2, a equação toma a forma
.
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
No ponto triplo coexistem três fases em equilíbrio. Como há apenas um componente, o número de graus de liberdade é dado por
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
ou seja, F = 0. Isso significa que nenhuma variável (temperatura ou pressão) pode ser mudada, mantendo-se a existência das três fases.
Ao longo de um contorno de fase, duas fases estão em equilíbrio, de modo que
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
e há apenas um grau de liberdade. Isso significa que para descrever o estado basta especificar apenas uma das variáveis, pois a outra já está definida.
Considerando um ponto situado em uma região com apenas uma fase,
o número de graus de liberdade nesse caso é 2. São necessárias duas variáveis para definir o estado do sistema.
Sistema binário
Para misturas binárias, há dois componentes (C = 2) e, além da temperatura e pressão, há a presença do grau de liberdade composição. Como muitas vezes as operações metalúrgicas, que fazem uso do diagrama binário, são realizadas à pressão atmosférica, a pressão é dada como constante a 1 atm, de modo que N = 1.[2]
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
Fluido supercrítico é qualquer substância em uma temperatura e pressão acima do seu ponto crítico, no qual não existe mais distinção entre as fases líquida e gasosa. Ele sofre efusão através de sólidos como um gás, e pode dissolver materiais como um líquido. Além disso, perto do seu ponto crítico, pequenas mudanças em sua pressão ou temperatura resultam em grandes mudanças de densidade, permitindo que sejam feitos pequenos ajustes nas propriedades de um fluido supercrítico.
Os fluidos supercríticos são substitutos adequados a solventes orgânicos em uma variedade de processos industriais e laboratoriais. Dióxido de Carbono e água são os fluidos supercríticos mais comumente usados, para descafeinação e geração de eletricidade, respectivamente.
Propriedades
Em termos gerais, fluidos supercríticos tem propriedades entre a de um gás e a de um líquido. Na Tabela 1, as propriedades críticas de alguns componentes que são comumente usados como fluidos supercríticos são mostradas.
Tabela 1. Propriedades críticas de vários solventes (Reid et al., 1987) Solvente Peso molecular Temperatura Crítica Pressão Crítica Densidade Crítica g/mol K MPa (atm) g/cm3 Dióxido de Carbono (CO2) 44.01 304.1 7.38 (72.8) 0.469 Água (H2O) 18.015 647.096 22.064 (217.755) 0.322 Metano (CH4) 16.04 190.4 4.60 (45.4) 0.162 Etano (C2H6) 30.07 305.3 4.87 (48.1) 0.203 Propano (C3H8) 44.09 369.8 4.25 (41.9) 0.217 Etileno (C2H4) 28.05 282.4 5.04 (49.7) 0.215 Propileno (C3H6) 42.08 364.9 4.60 (45.4) 0.232 Metanol (CH3OH) 32.04 512.6 8.09 (79.8) 0.272 Etanol (C2H5OH) 46.07 513.9 6.14 (60.6) 0.276 Acetona (C3H6O) 58.08 508.1 4.70 (46.4) 0.278 - ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
e
são as frações molares dos componente A e B e,
e :
são suas respectivas Temperaturas Críticas.
A Tabela 2 mostra densidade, coeficiente de difusão e viscosidade para gases, líquidos e fluidos supercríticos típicos.
Comparação de gases, fluidos supercríticos e líquidos[1] Densidade (kg/m3) Viscosidade (µPa∙s) Coeficiente de difusão (mm²/s) Gases 1 10 1–10 Fluidos supercríticos 100–1000 50–100 0.01–0.1 Líquidos 1000 500–1000 0.001 Além disso, não há tensão superficial em um fluido supercrítico, já que não há uma divisão entre as fases líquida e gasosa. Mudando a pressão e temperatura do fluido, as propriedades podem ser ajustadas para serem mais parecidas com as de um líquido ou de um gás. Uma das mais importantes propriedades é a solubilidade do material no fluido. Solubilidade num fluido supercrítico tende a aumentar com a densidade do fluido (a uma temperatura constante). Já que a densidade aumenta com a pressão, a solubilidade tende a aumentar com a pressão. A relação com a temperatura é mais complicada. À uma densidade constante, a solubilidade irá aumentar com a temperatura, no entanto, perto do ponto crítico, a densidade pode cair abruptamente com um pequeno aumento de temperatura. Portanto, perto da temperatura crítica, a solubilidade geralmente cai com um aumento de temperatura e então cresce de novo.[2]
Todos os fluidos supercríticos são completamente miscíveis uns com os outros, então para uma mistura uma única fase pode ser garantida se o seu ponto crítico for excedido. O ponto crítico de uma mistura de dois elementos pode ser estimada através da média aritmética das temperaturas e pressões críticas dos dois componentes.[3]
onde:
Para uma maior precisão, o ponto crítico pode ser calculado usando equações de estado, como as de Peng Robinson, ou métodos de contribuição de grupo. Outras propriedades, como a densidade, podem ser calculadas usando equações de estado.
Diagrama de fase
As figuras 1 e 2 mostram projeções de diagramas de fase. No diagrama de fase de pressão por temperatura (Fig. 1) as fases líquida e gasosa são separadas pela ebulição até o ponto crítico, onde essas duas fases somem e viram uma única fase supercrítica. Isso pode ser observado no diagrama de fase de pressão por densidade do dióxido de carbono, como mostra a Figura 2. Bem abaixo da temperatura crítica, como, por exemplo, à 280K, conforme a pressão aumenta, o gás é comprimido e eventualmente, a apenas 40 bar, condensa em um líquido muito mais denso, resultando na descontinuidade na linha (linha vertical pontilhada). O sistema consiste de duas fases em equilíbrio, um líquido de alta densidade e um gás de baixa densidade. Conforme se chega próximo à temperatura crítica (300K), a densidade do gás em equilíbrio se torna maior e a do líquido menor. No ponto crítico, (304.1 K e 7.38 MPa (73.8 bar)) não há diferença na densidade, e as duas fases se tornam uma única fase fluida. Portanto, acima da temperatura crítica, um gás não pode ser liquefeito através de pressão. Um pouco acima da temperatura crítica (310K), nas proximidades da pressão crítica, a linha é quase vertical. Um pequeno incremento na pressão causa um grande aumento na densidade da fase supercrítica. Muitas outras propriedades física também mostram grandes gradientes com a pressão perto do ponto crítico, como por exemplo, a viscosidade, a constante dielétrica e a força do solvente, que são intimamente relacionados com a densidade. Em temperaturas mais altas, o fluido começa a se comportar como um gás, como pode ser visto na Figura 2. Para o dióxido de carbono, a 400K, a densidade aumenta quase linearmente com a pressão.
Muitos gases pressurizados são na verdade fluidos supercríticos. Por exemplo, o Nitrogênio tem um ponto crítico de 126.2K (-147 °C) e 3.4 MPa (34 bar). Portanto, Nitrogênio (ou ar comprimido) em um cilindro de gás acima dessa temperatura é na verdade um fluido supercrítico. Estes são mais comumente conhecidos como gases permanentes. Em temperatura ambiente, eles estão bem acima de sua temperatura crítica, e portanto se comportam como um gás, como o CO2 a 400K e acima. No entanto, eles não podem ser liquefeitos por pressão a não ser que sejam resfriados abaixo de sua temperatura crítica.
Ocorrências Naturais
Vulcões submarinos
Vulcões submarinos são comuns no fundo oceânico. Alguns são ativos e, em águas rasas, mostram sua presença através de um jato de vapor e detritos muito acima da superfície do mar. Muitos outros ficam em profundidades tão grandes que a imensa pressão do peso da água sobre eles previne esses jatos explosivos de vapor e gases. Isso faz com que a água seja aquecida a mais de 375 °C, transformando a água nas partes mais quentes do vulcão em um fluido supercrítico, já que a pressão numa profundidade de 3 km é de mais de 300 atmosferas, bem acima das 218 atmosferas necessárias.
Atmosferas planetárias
A atmosfera de Vênus é 96.5% dióxido de carbono e 3.5% Nitrogênio. A pressão na sua superfície é de 9.3 MPa (93 bar) e a temperatura é de 735K, acima dos pontos críticos dos seus principais constituintes e fazendo a superfície de sua atmosfera um fluido supercrítico.
As atmosferas interiores dos gigantes gasosos do Sistema Solar são compostas principalmente de Hidrogênio e Hélio a temperaturas muito acima de seus pontos críticos. As atmosferas gasosas exteriores de Júpiter e Saturno se transicionam suavemente até o interior fluido dos planetas. Modelos teoréticos dos planetas extra solares 55 Cancri e e Gliese 876 d postularam um oceano de água pressurizada e supercrítica com uma camada de gelo sólido a uma alta pressão no fundo.
Denomina-se matéria degenerada, ou ainda gás degenerado, aquela na qual uma fração importante da pressão provém do princípio de exclusão de Pauli, que estabelece que dois férmions não podem ter os mesmos números quânticos.
Tal "gás" não obedece às leis clássicas segundo as quais a pressão de um gás é proporcional à sua temperatura e densidade.
Enrico Fermi e Paul Adrien Maurice Dirac provaram que, a uma densidade muito alta, a pressão aumenta rapidamente até o ponto em que ela passa a independer da temperatura do gás. Neste ponto, o gás passa a agir quase como um sólido.
Na astronomia, este gás é encontrado nas estrelas anãs brancas e é importante no tratamento tanto de estrelas residuais densas quanto das novas que as geram.[1] É conceito importante em cosmologia e na evolução do universo no tempo,[2] com relações com a teoria da relatividade[3] e para o modelo "big bang" e na detecção de objetos estelares.[4]
Dependendo das condições, a degeneração de diferentes partículas pode contribuir com a pressão de um objeto compacto, de modo que uma anã branca está sustentada pela degeneração dos elétrons, ainda que uma estrela de nêutrons não colapse devido ao efeito combinado da pressão de nêutrons degenerados e da pressão devida à ação repulsiva da interação forte entre bárions.
Estas restrições nos estados quânticos fazem com que as partículas adquiram momentos muito elevados, já que não têm outras posições do espaço de fases onde situar-se; pode-se dizer que o gás, ao não poder ocupar mais posições, se vê obrigado a estender-se no espaço de momentos com a limitação da velocidade c (velocidade da luz). Assim, ao estar tão comprimida a matéria, os estados energeticamente baixos preenchem-se em seguida, pelo que muitas partículas não têm outra possibilidade senão colocar-se em estados muito energéticos, o que envolve uma pressão adicional de origem quântica. Se a matéria está suficientemente degenerada, esta citada pressão será dominante, e muito, sobre todas as demais contribuições. Esta pressão é, além disto, independente da temperatura e unicamente dependente da densidade.
Estas características implicam tratamento termodinâmico bastante diverso e adequado às pressões e campos gravitacionais envolvidos,[5] assim como o comportamento das reações nucleares na proximidade de tais massas.[6][7]
Necessita-se de densidades para chegar aos estados de degeneração da matéria. Para a degeneração de elétrons se requer uma densidade em torno dos 106 g/cm³, para a de nêutrons necessita-se muito mais ainda, 1014 g/cm³.
Tratamento matemático da degeneração
Para calcular o número de partículas fermiônicas em função de seu momento, se usará a distribuição de Fermi-Dirac (ver estatística de Fermi-Dirac) da seguinte maneira:
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
Onde n(p) é o número de partículas com momento linear p. O coeficiente inicial 2 é a dupla degeneração de spin dos férmions. A primeira fração é o volume do espaço de fases em um diferencial de momentos dividido pelo volume de uma determinada seção no espaço. A h³ é a constante de Planck ao cubo que, como se tem dito, significa o volume dessas seções nas quais cabem até duas partículas com spins opostos. O último termo fracionário é o denominado fator de preenchimento. K é a constante de Boltzmann, T a temperatura, Ep a energia cinética de uma partícula com momento p e ψ o parâmetro de degeneração, que é dependente da densidade e da temperatura.
- O fator de preenchimento indica a probabilidade de este preencher um estado. Seu valor está compreendido entre 0 (todos vazios) e 1 (todos preenchidos).
- O parâmetro de degeneração indica o grau de degeneração das partículas. Se toma valores grandes e negativos a matéria estará em um regime de gás ideal. Se está próximo a 0 a degeneração se começa a notar. Diz-se que o material está parcialmente degenerado. Se o valor é grande e positivo o material está altamente degenerado. Isto acontece quando as densidades são elevadas ou também quando as temperaturas são baixas.
Desta equação se podem deduzir as integrais do número de partículas, a pressão que exercem e a energia que têm. Estas integrais são possíveis de serem resolvidas analiticamente quando a degeneração é completa.
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
- Matéria degenerada não relativista (NR):
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
- Matéria degenerada extremamente relativista (ER):
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
pressões obtidas com a degeneração completa não relativista. É lógico, já que a matéria relativista é mais quente.
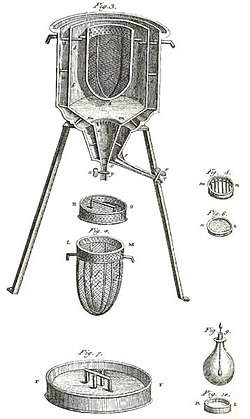 Primeiro calorímetro de gelo do mundo, usado no inverno de 1782–83 por Antoine Lavoisier e Pierre-Simon Laplace, para determinar o calor envolvido em várias alteração química, que eram baseados na descoberta anterior de Joseph Black do calor latente. Esse experimentos marcam a fundação da termoquímica
Primeiro calorímetro de gelo do mundo, usado no inverno de 1782–83 por Antoine Lavoisier e Pierre-Simon Laplace, para determinar o calor envolvido em várias alteração química, que eram baseados na descoberta anterior de Joseph Black do calor latente. Esse experimentos marcam a fundação da termoquímicaA termoquímica, também chamada de termodinâmica química, é o ramo da físico-química que estuda as quantidades de calor (energia) absorvidas ou liberadas em reações químicas, assim como as transformações físicas, tais como a fusão e a ebulição, baseando-se em princípios da termodinâmica.[1][2][3][4][5]
A termoquímica genericamente é relacionada com a troca de energia acompanhando transformações, tais como misturas, transições de fases, reações químicas, além de calcular grandezas como a capacidade térmica, o calor de combustão, o calor de formação, a entalpia e a energia livre.[1][6]
História
A termoquímica apoia-se sobre duas generalizações:[7]
- Leis de Lavoisier e Laplace (1780): A transferência de energia acompanhando qualquer transformação é igual e oposta à transferência de energia acompanhando o processo reverso.[8]
- Lei de Hess (1840): A variação de energia (entalpia) total de uma reação é a soma das entalpias de reação das etapas em que a reação pode ser dividida.[9]
Gustav Kirchhoff mostrou em 1858 que a variação do calor de reação é dada pela diferença da capacidade térmica entre os produtos e os reagentes: dΔH / dT = ΔCp. A integração dessa equação permite avaliar o calor de reação a uma temperatura a partir de valores em outra temperatura.[10][11]
Princípios

Princípios da Química Calor e calorimetria
As transformações físicas e as reações químicas são, geralmente, acompanhadas pela liberação ou absorção de calor. Sabe-se, por exemplo, que é necessário fornecer calor (energia) para que a água seja aquecida a ponto de se vaporizar; e que, por outro lado, há liberação de calor (energia) quando o vapor da água se condensa. Percebe-se a enorme importância de se conhecer e controlar essas trocas de calor, por exemplo, no funcionamento das locomotivas a vapor, um dos avanços tecnológicos centrais da primeira revolução industrial, que transformava a energia térmica em trabalho.[1]
A calorimetria é o estudo e a medição das quantidades de calor liberadas ou absorvidas pelos fenômenos físicos e químicos.[12] Para o desenvolvimento experimental da medição do calor, foram construídos os calorímetros, aparelhos utilizados para efetivamente medir o calor trocado. Um dos mais simples calorímetros é o calorímetro de água, em que se coloca um corpo aquecido (ou que provoque uma reação química) dentro da água contida pelo calorímetro, resultando em seu aquecimento. Conhecendo o quanto a temperatura da água se elevou, é possível determinar a quantidade de calor liberada pelo corpo ou pela reação, contanto que a troca de calor com o ambiente externo seja desprezível. Com isso, percebe-se que o aumento de temperatura da água é devido exclusivamente ao corpo aquecido ou à reação ocorrida, isto é, o calor recebido pela água é, em módulo, igual ao calor cedido pelo corpo ou pela reação. Portanto, denominando-se por
a massa de água do calorímetro, por
o calor específico da água, e por
a variação na temperatura da água, temos que o calor trocado
é tal que:[13]
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
O valor da energia das partículas dependerá da velocidade das partículas, a qual decidirá se se tem-se um gás relativista ou não. No primeiro caso se usarão as equações de Einstein e no segundo valerá a aproximação clássica. Como se pode ver, as relações energia-pressão variam significativamente, sendo maiores as
As estrelas típicas com degeneração são as anãs brancas e as anãs marrons sustentadas por elétrons e as estrelas de nêutrons sustentadas por nêutrons degenerados. Considera-se que sua temperatura tende a 0, já que não possuem fonte de calor alguma. Suporemos estes corpos com um parâmetro de degeneração tendente a +infinito.
Energia interna
Na física da mecânica clássica, existem fundamentalmente dois tipos de energia que um objeto pode ter:
- A energia cinética, associada ao seu movimento;
- A energia potencial, por ele armazenada e que pode se transformar em outro tipo de energia, cinética ou potencial.
Desse modo, é possível entender o calor liberado ou absorvido por uma reação química a partir do conceito de energia interna. A energia interna de uma substância qualquer, composta por átomos e/ou moléculas, é equivalente a soma da energia química armazenada por ligações elétricas entre átomos e entre moléculas (uma forma de energia potencial), e da energia térmica armazenada na translação, vibração ou rotação de átomos e moléculas (uma forma de energia cinética). Isto é, a energia interna de uma substância é armazenada parcialmente na forma de energia química e parcialmente na forma de energia térmica.[14]
Tomando a generalização do conceito de energia interna de uma substância como sendo a energia interna de um sistema, a soma de todas as energias internas das substâncias que o compõem, enuncia-se então a lei da conservação de energia ou a primeira lei da termodinâmica para um sistema isolado, que não troca calor, e nem sofre nem exerce trabalho. Essa lei afirma que a variação da energia interna de um sistema isolado é nula, ou, de forma equivalente, a energia interna de um sistema isolado é constante.[14]
Entalpia
Entalpia é um conceito ligado a termodinâmica que serve para quantificar a quantidade de energia que uma substância contém. A entalpia é uma função de estado, uma propriedade extensiva ( proporcional a quantidade de mol).
Para definir a entalpia, é conveniente tomar o exemplo da queima de carvão em um ambiente aberto. Nele, o carbono (


- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
Em uma análise preliminar, percebe-se que o volume do sistema aumentou, pois, já que o volume do carbono sólido era desprezível, havia 1 mol 

Portanto, parte da energia liberada na reação foi utilizada para expandir o gás na forma de trabalho. Como decorrência da conservação de energia, esse trabalho de expansão deverá ser "descontado" da energia liberada pela reação, resultando em um "saldo" menor da energia. Denomina-se esse "saldo" por entalpia (
Com isso, a variação de entalpia (


, a
constante
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
Reações exotérmicas e endotérmicas
Reações exotérmicas são as reações que produzem ou liberam calor, como por exemplo a queima de carvão e a combustão da gasolina.[1] Nelas, a entalpia dos reagentes é maior que a entalpia dos produtos, resultando em uma variação negativa de entalpia (

Como exemplo comparativo, a reação que tem como produto H2O é exotérmica, pois libera calor. Já a reação inversa é endotérmica, porque necessita de calor para que se gerem os produtos:[15]
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
Energia de ativação
A energia de ativação é a menor quantidade de energia necessária que deve ser fornecida aos reagentes para a formação do complexo ativado e para a ocorrência da reação.
A entropia (do grego εντροπία, entropía), unidade [J/K] (joules por kelvin), é uma grandeza termodinâmica que mede o grau de liberdade molecular de um sistema,[1] e está associado ao seu número de configurações (ou microestados), ou seja, de quantas maneiras as partículas (átomos, íons ou moléculas) podem se distribuir em níveis energéticos quantizados, incluindo translacionais, vibracionais, rotacionais, e eletrônicos. Entropia também é geralmente associada a aleatoriedade, dispersão de matéria e energia, e "desordem" (não em senso comum)[Nota 1] de um sistema termodinâmico. A entropia é a entidade física que rege a segunda lei da termodinâmica, a qual estabelece que a ela deve aumentar para processos espontâneos e em sistemas isolados. Para sistemas abertos, deve-se estabelecer que a entropia do universo (sistema e suas vizinhanças) deve aumentar devido ao processo espontâneo até o meio formado por sistema + vizinhanças atingir um valor máximo no estado de equilíbrio. Nesse ponto, é importante ressaltar que vizinhanças se entende como a parte do resto do universo capaz de interagir com o sistema, através de, por exemplo, trocas de calor. [2]
A segunda lei da termodinâmica foi primeiramente relacionada historicamente com processos cíclicos que convertiam calor em trabalho. Percebeu-se que energia térmica (calor) não poderia ser completamente convertida em trabalho em máquinas térmicas de motor perpétuo, sempre havendo a necessidade de perda de uma quantidade mínima de calor para um reservatório frio para que o sistema voltasse ao estado original. Dessa maneira, a variação de entropia de um processo está relacionada com a parcela de energia que não pode ser transformada em trabalho em transformações termodinâmicas a dada temperatura. Por esse fato, a mensuração da variação de entropia está diretamente relacionada a processos reversíveis, uma vez que processos no equilíbrio (ou mais próximos possíveis às condições de equilíbrio) estão associados com a máxima energia que um sistema pode perder para as vizinhanças na forma de trabalho (chamado de trabalho máximo ou trabalho útil). Portanto a energia "não disponível" é o mínimo valor que não pode seria descartado na forma de calor reversível em um processo que ocorre espontaneamente. Em outras palavras, a variação de entropia mede o grau de irreversibilidade de um processo.
A parcela máxima de energia interna de um sistema pode mais ser convertida em trabalho em um dado processo pode ser determinada pelo produto da variação de energia interna do processo subtraído do produto da variação entropia S pela temperatura absoluta T do sistema no respectivo estado (desde que a temperatura constante). Essa parcela máxima de energia é conhecida como variação de energia livre de Helmholtz (ΔA). Dessa maneira, define-se a energia livre de Helmholtz como 
A entropia não é uma grandeza que busca mensurar a energia ou a matéria totais encerradas pelas fronteiras do sistema termodinâmico, mas sim como esta matéria e esta energia encontram-se armazenadas e distribuídas no sistema definido por tais fronteiras. Assim, embora uma grandeza bem distinta das grandezas massa, energia interna e quantidade de matéria, a entropia de um sistema encontra-se certamente relacionada às grandezas citadas, sendo, da mesma forma que as anteriores, uma propriedade do sistema. A fim de definir-se um sistema simples especificam-se a energia interna U, a massa m - especificamente a quantidade de matéria N e a natureza das partículas que integram o sistema - e o seu volume V, e ao fazê-lo determina-se também, de forma automática, o valor da entropia S do sistema - uma grandeza escalar - no estado final a ser atingido uma vez dado tempo suficiente para que todos os processos necessários aconteçam. Assim a entropia S nos estados de equilíbrio termodinâmico é uma função das grandezas antes citadas: 
Assim, segundo a Segunda Lei da Termodinâmica, processos que levam o sistema do estado inicial, logo após ter sido isolado, até o estado de final (o estado de equilíbrio termodinâmico ) ocorrem sempre de forma a provocarem aumentos ou, no limite, a manutenção, do valor da entropia do sistema. Não ocorrem processos que impliquem a diminuição da entropia total de um sistema isolado. A entropia é, pois, uma função de estado que obedece a um princípio de maximização, o "princípio da máxima entropia": a entropia em um estado de equilíbrio termodinâmico - satisfeitas as restrições impostas ao sistema - é sempre a máxima possível. Portanto, sistemas fora do equilíbrio tendem a caminhar irreversivelmente para o estado de equilíbrio, e o aumento de entropia indicará o sentido espontâneo do processo.
A entropia é uma função de estado cujo valor sempre cresce durante processos naturais em sistemas isolados; e quando escrita em função das grandezas extensivas energia interna U, volume V e número de elementos N - no caso dos sistemas termodinâmicos mais simples - a entropia 
Se expressa em função de uma ou mais grandezas que não as citadas - cônjuges a si - a expressão para a entropia S reduz-se a uma mera equação de estado. As equações de estado, embora relacionem valores de grandezas termodinâmicas nos estados de equilíbrio, não retêm em si, individualmente, todas as informações acerca do sistema. É necessário o conhecimento de todas as equações de estado para recuperar-se a completeza acerca das informações - para a partir delas se estabelecer uma equação fundamental - e via transformada de Legendre, se estabelecer qualquer das demais equações fundamentais - se desejada.
Conceitos científicos de "desordem"
A associação vaga de entropia com "desordem" ao considerar-se o sentido em senso comum desta palavra leva muitas vezes a uma compreensão errônea da definição de entropia e também a usos completamente inadequados da segunda lei da termodinâmica,[Nota 2] e assim, vale estabelecer-se aqui pelo menos um conceito aceitável para o termo "desordem" que seja adequado ao meio científico.
Segundo a física estatística a desordem de um sistema pode ser associada - não diretamente mas mediante uma função logaritmo - ao número de microestados acessíveis ao sistema uma vez satisfeitas as restrições impostas a ele. Restrições práticas comuns em sistemas termodinâmicos ligam-se geralmente ao valor da energia interna U e ao volume V disponíveis ao sistema, e aumentar a desordem de um sistema significa aumentar o número de microestados (de configurações) acessíveis às partículas deste sistema.
Um exemplo elucidador mas não exatamente análogo seria o que se obtém quando considera-se um baralho. Imposta a restrição de que todas as suas 54 cartas estejam em uma dada ordem pré-estabelecida, há apenas uma possibilidade de sequência para as cartas, ou seja, há apenas um microestado acessível a este sistema. Sua entropia seria, portanto, zero (pois ln 1 = 0). O número de microestados sobe para 54 se permitir-se que apenas uma dada carta esteja fora da ordem, e é significativamente maior se considerada a restrição de que apenas a primeira carta na sequência seja um ás. Se a restrição for relaxada ainda mais, impondo-se apenas que as cartas sejam as cartas de um único baralho completo (restrição antes também subentendida) o sistema terá o maior número de configurações possíveis, a maior desordem possível, e portanto a maior entropia possível. Aumentar a desordem, ou seja, a entropia de um sistema termodinâmico significa, de forma similar, dar-lhe condições para que haja um maior número de microestados acessíveis às partículas que o compõem.
A comparação com o baralho não é direta pois em sistemas termodinâmicos há de se considerar a indistinguibilidade das partículas (o que não ocorre com as cartas) e o que vem a ser um microestado, ou seja, uma configuração do sistema, entre outros pormenores, mas de forma geral, assim como ocorre para o baralho, a remoção de restrições impostas ao sistema em equilíbrio leva a um aumento na sua entropia. Importante também é observar que um aumento da energia interna U mantidas as restrições espaciais leva a um aumento de microestados acessíveis às partículas do sistema pois estas têm, agora, mais energia, e portanto a um aumento na entropia deste. A entropia cresce com a energia interna U de forma monótona para sistemas estáveis, o que significa dizer, em acordo com a definição de temperatura [Nota 3]absoluta, que, para sistemas em equilíbrio, a temperatura absoluta nunca pode ser negativa.
Há em verdade várias interpretações cientificamente corretas para o termo "desordem", e citar-se-á também uma oriunda da termodinâmica e diretamente associada à segunda lei da termodinâmica e ao estudo da máquina térmica e das transformações de energia (calor e trabalho) nestas máquinas. A segunda lei obriga que uma máquina térmica (ou um refrigerador) tenha necessariamente uma fonte quente e uma fonte fria. Um aumento da entropia representa, em tais sistemas, uma medida da energia que, oriunda da fonte quente, poderia ter sido aproveitada na forma de trabalho, mas, não o sendo, foi simplesmente "desperdiçada" como calor na fonte fria, tornado-se doravante indisponível para produzir o citado trabalho. A associação com desordem provém da observação de que trabalho em física envolve necessariamente variação de volume de uma parte do sistema, ou seja, o movimento direcionado de uma fronteira restritiva interna ao sistema isolado (a fronteira comum entre dois de seus subsistemas), e por conseguinte movimento direcionado, ordenado, de todas as partículas do subsistema delimitado por esta fronteira em movimento. Trabalho tem assim a ver com transferência de energia cinética (energia térmica), mas as partículas responsáveis por esta transferência movem-se de forma ordenada, direcionada, "acompanhando" a fronteira em movimento. Já a energia térmica trocada na forma de calor implica também variação da energia de movimento das partículas dos subsistemas, mas estas partículas agora movem-se de forma completamente desordenadas durante esta troca. O calor, oposto ao trabalho, implica a "propagação" de energia térmica mediante movimentos aleatórios - transferência de energia térmica (cinética) em forma não espacialmente direcionada -, feito de forma que a fronteira do sistema efetivamente não se move (o calor "passa" pela fronteira). Assim, o aumento de entropia, e portanto da desordem, de um sistema significa transformar parte do "movimento ordenado" das partículas de um sistema - que poderia ser usado para fazer trabalho - em movimento "desordenado", não associado a trabalho. O calor é a forma mais evidente de se fazer a entropia do sistema variar, ao passo que a troca de energia mediante trabalho por si só não implica variação da entropia, conforme visto.
Aumentar a desordem significa, assim, desperdiçar energia que poderia em princípio ser aproveitada como trabalho e, não o sendo, foi simplesmente entregue na forma de calor à fonte fria do sistema. Uma vez entregue à fonte fria, a energia atrelada ao aumento de entropia não pode mais, em contexto global, ser convertida em trabalho.
Transformações
Transformações reversíveis

A ideia de entropia, uma grandeza física que encontra sua definição dentro da área da termodinâmica,[Nota 4] surgiu no seguimento de uma função criada por Clausius[4] a partir de um processo cíclico reversível. Sendo Q o calor trocado entre o sistema e sua vizinhança, e T a temperatura absoluta do sistema, em todo processo reversível a integral de curva de 
,
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
- sendo Q reversível
A entropia física, em sua forma clássica é dada por:
,
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
- desde que o calor seja trocado de forma reversível
ou, quando o processo é isotérmico:
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
onde S é a entropia, 
O significado desta equação pode ser descrito, em linguagem corrente, da seguinte forma:
- Em processos reversíveis como o descrito, quando um sistema termodinâmico passa do estado 1 ao estado 2, a variação em sua entropia é igual à variação da quantidade de calor trocada (de forma reversível) dividido pela temperatura.
Processos de não equilíbrio
Em processos mais complexos, o que inclui os processos irreversíveis e de não equilíbrio como a expansão livre, entropia pode e sempre é produzida dentro do próprio sistema, e a variação total na entropia destes sistemas é igual à soma de dois termos: a entropia produzida e a entropia trocada com a vizinhança. A entropia trocada equivale, em processos quase estáticos, conforme descrito, à integral de dQ/T, sendo sempre nula quando a transformação é adiabática. O uso desta expressão ao casos de processos de não equilíbrio é contudo inadequado, ou, no mínimo, requer muita cautela, visto que a própria definição de temperatura fica comprometida. Já a entropia produzida vale zero apenas quando o processo é reversível, sendo sempre positiva em transformações irreversíveis.
Observa-se que em todas os processos a entropia total do sistema mais vizinhança ou aumenta (processos irreversíveis), ou fica constante (transformações reversíveis). Na prática, apesar de existirem processos que muito se aproximam dos reversíveis, toda transformação leva a um aumento na entropia total do sistema mais vizinhança, e este princípio permite definir a Segunda Lei da Termodinâmica, cuja implicação direta consiste no fato de que um processo tende a dar-se de forma espontânea em único sentido, aquele que leve ao aumento da entropia total (do sistema mais vizinhança). Por esses motivos, a entropia também é chamada de flecha do tempo.
Como não é possível determinar-se o aumento da entropia partindo-se diretamente de considerações sobre os sistemas que estão em processos de não equilíbrio - irreversíveis - justamente por estes estarem fora do equilíbrio, para determinar-se a variação de entropia total sofrida por um sistema ao longo de um processo de não equilíbrio determina-se a diferença entre as entropias inicial e final associadas aos respectivos estados de equilíbrio inicial e final. Tal consideração leva em conta o fato de a entropia ser uma função de estado, e por tal sua variação não depende de como o sistema saiu de um estado e chegou ao outro, e sim apenas dos estados inicial e final envolvidos.
A unidade de entropia no SI é designada por J/K'.
Definição termodinâmica
No início da década de 1850, Rudolf Clausius descreveu o conceito de energia desperdiçada em termos de diferenciais.
Em 1876, o físico, químico e matemático Willard Gibbs chegou à conclusão de que o conceito de energia disponível ΔG em um sistema termodinâmico é matematicamente obtido através da subtração entre a energia perdida TΔS e a variação da energia total do sistema ΔH.
Estes conceitos foram desenvolvidos posteriormente por James Clerk Maxwell 1871 e Max Planck 1903.
Nos dias de hoje a entropia é postulada conforme se segue: [Nota 6]
- - "Existe uma função (denominada entropia S) dos parâmetros extensivos de um sistema definida para todos os estados de equilíbrio termodinâmico deste sistema e com a seguinte propriedade: dentre todos os estados de equilíbrio possíveis que satisfazem as restrições físicas impostas ao sistema o estado de equilíbrio assumido pelo sistema será aquele para o qual os valores dos parâmetros extensivos neste estado levem à maximização do valor de sua entropia S. Em um sistema sem restrições internas a entropia é a maior possível."
A exemplo, na parte superior da figura ao lado tem-se um sistema com uma fronteira adiabática e uma restrição interna. O estado de equilíbrio termodinâmico de um sistema, satisfeitas as restrições internas, corresponde ao estado onde a entropia é a máxima possível. Na parte inferior a restrição é removida. O sistema passa por transformações e, após certo tempo atinge um novo estado de equilíbrio termodinâmico. Nestas transformações a entropia do sistema geralmente aumenta, o que ocorre para expansão livre mostrada, ou em casos outrem específicos - quando todos os processos se fazem de forma reversível - não se altera. A entropia de um sistema isolado nunca diminui.
Assim, o estado de equilíbrio realmente assumido por um sistema termodinâmico é, satisfeitas as restrições físicas impostas, o estado de maior entropia possível, e a remoção de uma restrição leva geralmente a um aumento da entropia do sistema composto, ou, em caso específicos (transformações reversíveis), à manutenção de seu valor, mas nunca a uma diminuição da mesma.
Há três outros postulados que, em termodinâmica, mostram-se diretamente associados à definição de entropia, sendo eles:
- - "A entropia de um sistema composto é aditiva sobre os subsistemas que o constituem. A entropia é contínua e diferenciável e é uma função monótona crescente da energia interna U."
- - "A entropia de um sistema é nula para um estado onde a temperatura absoluta T também o seja."
- - "Existe um estado particular - chamado estado de equilíbrio - de um sistema que, macroscopicamente, é completamente caracterizado pela energia interna U, pelo volume V, e pela quantidade de matéria N1, N2,N3 de seus constituintes químicos.".[Nota 7]
A entropia S quando expressa em função do volume V do sistema, da quantidade de partículas N do sistema e da energia interna U do sistema, S(U,N,V), é uma Equação Termodinâmica Fundamental para um sistema termodinâmico simples, e pode, mediante a Transformada de Legendre, ser transformada em outras equações fundamentais como a equação da Entalpia H(S,P,N), Energia de Helmholtz F(T,V,N), Energia livre de Gibbs G(T,P,N) ou o Grande Potencial Canônico U(T,P,m). Em sistemas termodinâmicos mais complexos, a exemplo em sistemas magnéticos, outras variáveis podem vir a figurar na equação entrópica fundamental e nas outras equações fundamentais, entretanto os conceitos de equação fundamental e transformada de Legendre permanecem os mesmos.
As equações fundamentais diferem das equações de estado basicamente no fato de que a partir de uma equação fundamental pode-se obter, com o uso do formalismo termodinâmico, qualquer informação a respeito do sistema termodinâmico por ela descrito, inclusive as equações de estado para este sistema, ao passo que o mesmo não pode ser feito a partir de uma equação de estado, que não retém em si todas as informações necessárias a respeito do sistema. É necessário um conjunto de equações de estado para a descrição completa de um sistema termodinâmico (do qual poderia obter-se, então, as equações fundamentais).
Primeira Lei da Termodinâmica
A primeira lei da termodinâmica é a lei de conservação de energia aplicada aos processos térmicos. Nela observamos a equivalência entre trabalho e calor. Este princípio pode ser enunciado a partir do conceito de energia interna. Esta pode ser entendida como a energia associada aos átomos e moléculas em seus movimentos e interações internas ao sistema. Num sistema isolado a energia total permanece constante.[Nota 8]
Segunda Lei da Termodinâmica
A Segunda Lei da Termodinâmica, uma importante lei física, determina que a entropia total de um sistema termodinâmico isolado tende a aumentar com o tempo, aproximando-se de um valor máximo à medida que restrições internas ao sistema são removidas. O estado de equilíbrio termodinâmico de um sistema isolado corresponde ao estado onde, satisfeitas as restrições internas, a entropia é máxima. Duas importantes consequências disso são que o calor não pode passar naturalmente de um corpo frio a um corpo quente, e que um Moto perpétuo, ou seja, um motor que produza trabalho infinitamente (ou seja, em processos cíclicos) a partir de uma fonte quente seja impossível.[Nota 9] Isso acarreta que nenhuma máquina térmica tenha rendimento de 100%, pois sempre é necessário um desperdício irreversível de calor para uma fonte fria para o sistema voltar ao estado original e, assim, continue a produzir trabalho a partir do recebimento de calor da fonte quente.
Interpretação estatística
Em 1877, Ludwig Boltzmann visualizou um método probabilístico para medir a entropia de um determinado número de partículas de um gás ideal, na qual ele definiu entropia como proporcional ao logaritmo neperiano do número de microestados que um gás pode ocupar:
- ////
- sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
Onde S é a entropia, k é a constante de Boltzmann e Ω é o número de microestados possíveis para o sistema.
O trabalho de Boltzmann consistiu em encontrar uma forma de obter a equação entrópica fundamental S a partir de um tratamento matemático-probabilístico[Nota 10] facilmente aplicável aos sistemas em questão. Ao fazê-lo, conectou o todo poderoso formalismo termodinâmico associado à equação fundamental a um método de tratamento probabilístico simples que exige apenas considerações físicas primárias sobre o sistema em análise, obtendo, a partir de considerações básicas, todo o comportamento termodinâmico do sistema. A equação de Boltzman mostra-se muito importante para o estudo termodinâmico de tais sistemas, e reconhecida como tal pelo próprio autor, encontra-se gravada em sua lápide.[Nota 11]
Força associada à entropia
Qual é a origem da força entrópica? A resposta mais geral é que um sistema sempre quer retornar ao seu estado de máxima entropia, isso explica porque as moléculas tendem a resistir sair do seu estado de desordem.
Em física, uma força entrópica atuando em um sistema é uma força resultante da tendência termodinâmica de todo o sistema para aumentar sua entropia. A abordagem entrópica para o movimento browniano foi inicialmente proposta por RM Neumann,[5] Neumann associou a força entrópica de uma partícula em movimento browniano tridimensional usando a equação de Boltzmann e denotou esta força como uma força motriz.
Formulação matemática
A dedução dessa fórmula parte da primeira lei da termodinâmica e da definição de trabalho, considerando dilatações pequenas podemos escrever a primeira lei na forma:
No entanto, se a dilatação total objeto (dE) for pequena e a considerarmos igual à zero, obtemos a expressão para a força exercida pelo elástico:
Polímeros
Podemos sentir o efeito da entropia ao esticarmos um elástico, por exemplo. A borracha é formada por longas cadeias de polímeros com ligações cruzadas – que lembram ziguezagues. Quando o elástico está relaxado essas cadeias estão parcialmente enroladas e ordenadas aleatoriamente, devido a esse alto grau de desordem das moléculas o estado possui um valor de entropia também alto. Ao esticarmos o elástico desenrolamos essas moléculas e as alinhamos, como o alinhamento diminui a desordem isso significa dizer que a derivada 
Força hidrofóbica
Outro exemplo de força entrópica são as interações hidrofóbicas. Elas ocorrem em função do aumento da entropia (∆S) do sistema proveniente da liberação das moléculas de água, quando dois átomos apolares interagem. As interações hidrofóbicas possuem papel importante na estabilização de complexos entre ligantes e receptores, como acontece nas proteínas (macromoléculas formada pela união de uma sequência de aminoácidos), onde as cadeias hidrofílicas ficam no exterior e as cadeias hidrofóbicas ficam no interior da proteína, dando conformação a macromolécula, como um envelopamento da molécula.
Gravidade
A gravidade tem sido considerada pela física moderna uma força entrópica. Erik Verlinde alegou que a gravidade é uma consequência da "informação associada com as posições dos corpos materiais". Isso implica que a gravidade não é uma força fundamental , mas um fenômeno emergente.
Entropia Genética
Os seres vivos em sua evolução assumida historicamente, foram entendidos como contrariando a lei da entropia física por se evoluírem e se manterem, pelo menos até o envelhecimento, ordenados em meio ao caos , graças a maquinarias moleculares capazes de enfrentar a tendência a desordem. Contudo cientistas como Basener, John C. Sanford[6][7][8][9] observaram que a nível populacional nas descendências está ocorrendo um acúmulo contínuo e sutil de desordens (mutações deletérias) e alguns autores ao medirem quantas mutações positivas ocorriam para as deletérias, chegaram a números alarmantes como 1 positiva para cada milhão de mutações (maioria negativas), "pode-se inferir que a proporção de mutações que são benéficas é cerca de um em um milhão"[10] explicando assim uma queda percentual na saúde em 11%[11] na inteligência humana[12]
Superfícies isentrópicas
Superfícies isentrópicas são superfícies formadas por todos os pontos que apresentem, em um diagrama de estados — onde os eixos coordenados estão associados às grandezas termodinâmicas como pressão, volume e temperatura (etc.), e cada ponto representa um possível estado de equilíbrio termodinâmico do sistema —, o mesmo valor para a entropia S.
Transformações sofridas pelo sistema são expressas como linhas unindo uma sequência de pontos no diagrama de estados, ou como "saltos" entre estes pontos.
Para um sistema isolado que sofra apenas transformações reversíveis, as linhas que representam as mudanças de estado estão restritas à superfície isentrópica à qual pertence o estado inicial. O sistema pode ser levado de um estado inicial a qualquer outro estado representado por ponto sobre a mesma isentópica sem comprometer a possibilidade de retorno ao estado inicial, feita também sobre a mesma superfície isentrópica.
Transformações irreversíveis em sistemas isolados (como a expansão livre) conectam pontos em isentrópicas distintas. Uma vez descrito por ponto em outra isentrópica (de valor S maior), o sistema isolado jamais poderá retornar ao estado inicial, ficando todos os estados associados à isentrópica anterior inacessíveis ao sistema isolado, que agora pode assumir apenas configurações descritas por pontos na sua nova isentrópica, ou em isentrópicas superiores (com maiores valores de S).
O retorno do sistema a isentrópicas com menores valores de S só é possível mediante a troca de calor e de entropia com a vizinhança, e assim, neste caso, o sistema não poderá mais estar adiabaticamente isolado. Tem-se então, em acordo com a Segunda Lei da Termodinâmica, uma redução na entropia do sistema às custas de um aumento na entropia global do conjunto sistema mais vizinhança.
Escoamentos isentrópicos são uma boa aproximação para os escoamentos atmosféricos reais em escala sinótica, nas regiões sem precipitação (por exemplo, nos escoamentos anticiclônicos, anti-horários no Hemisfério Sul e horários no Hemisfério Norte) e em equilíbrio radiativo (o ganho é igual à perda da densidade de fluxo radiativo).
Entalpia, por vezes referida como entalpia absoluta, é uma grandeza física definida no âmbito da termodinâmica clássica, de forma que esta meça a máxima energia de um sistema termodinâmico, teoricamente passível de ser deste removida na forma de calor. É particularmente útil na compreensão e descrição de processos isobáricos:[1] à pressão constante as variações de entalpia encontram-se diretamente associadas às energias recebidas pelo sistema na forma de calor, as quais são facilmente mensuráveis em calorímetros.
Conforme definida, a entalpia engloba em si não apenas a energia interna do sistema, mas também a energia armazenada no conjunto sistema-vizinhança que, absorvida pelo sistema via trabalho realizado pela vizinhança em processos termodinâmicos que impliquem a diminuição de seu volume, também integra uma parcela de energia passível de ser extraída na forma de calor a partir do referido sistema. A entalpia mensura pois a totalidade de energia de alguma forma atrelada ao sistema - incluindo-se nesta não apenas a energia encerrada no sistema como também a energia atrelada ao sistema em virtude das relações que este estabelece com a sua vizinhança.
Em acordo com o apresentado, a variação de entalpia, define-se por:[2][3]
onde U representa a energia interna do sistema e PV mensura a quantidade de energia associada ao conjunto sistema-vizinhança devido ao fato do sistema ocupar um volume V quando submetido à pressão constante P, ou seja, o máximo trabalho executável pela vizinhança sobre o sistema.
Embora as entalpias absolutas - assim como as energias internas absolutas - não desempenhem papel de maior relevância na análise prática de processos físico-químicos - sendo em verdade experimentalmente muito complicadas suas precisas determinações - as variações de entalpia são contudo facilmente mensuráveis via aparelhos conhecidos como calorímetros e estas sim desempenham papel o mais importante na análise dos citados processos. É a variação de entalpia 
A entalpia-padrão de um sistema corresponde à entalpia do sistema antes descrita subtraída de uma constante adequadamente escolhida de forma a ter-se a entalpia-padrão de um sistema em particular - adequadamente escolhido para constituir um padrão universal de referência - propositalmente definida como zero. A definição de entalpia-padrão faz-se por razões práticas e não acarreta implicação alguma na determinação das variações de entalpia em processos termodinâmicos, visto serem as suas variações iguais às respectivas variações de entalpia absoluta (
No Sistema Internacional de Unidades a unidade da entalpia é o joule (J). Ao passo que na literatura a entalpia absoluta é geralmente representada pelo símbolo H, a entalpia-padrão encontra-se geralmente representada pelo símbolo H 0.
Quando expressa em função da entropia S, número de elementos N, e da pressão P - para o caso de sistemas termodinâmicos mais simples - a entalpia 



Índice
Definição
Quando um sistema imerso em um ambiente à pressão constante sofre um processo qualquer, indo de um estado inicial "i" para um estado final "f", a quantidade de energia trocada com a vizinhança na forma de trabalho é definida apenas pela variação de volume 
É de interesse mensurar neste tipo de transformação a quantidade de calor trocada entre o sistema e sua vizinhança. Ao ceder-se certa quantidade de calor ao sistema, este expande-se, realizando um trabalho W sobre a vizinhança. A energia entregue à vizinhança - e que por tal abandona o sistema - é transferida às custas de parte do calor que entra no sistema, de forma que apenas parte do calor transferido ao sistema implica real aumento na energia interna deste sistema. A lei da conservação da energia fornece:
Como a energia interna e o volume do sistema são funções de estado, segue-se que nestes processos a quantidade de calor trocada também é uma função de estado. A expressão acima permite a definição de uma grandeza física conhecida por entalpia H de forma que:
Decorre que a entalpia pode ser definida pela função de estado introduzida por Josiah Willard Gibbs:
Definição de Entalpia
onde U é a energia interna do sistema e PV é o produto da pressão pelo volume do sistema (e da vizinhança), ou seja, a energia armazenada no conjunto sistema vizinhança.
Conforme definida, a variação da entalpia implica pois a expressão antes apresentada para a conservação da energia:
A entalpia, por ser - assim como a energia interna e o trabalho - uma grandeza associada à medida de energia, é por tal também medida em joules.
É aqui importante ressaltar-se que a variação da entalpia em um dado processo corresponde sempre à entalpia do estado final menos a entalpia do estado inicial atrelados ao referido processo, e que em equações químicas esta corresponde pois a entalpia do estado onde tem-se os produtos menos a entalpia do estado onde tem-se os reagentes (
Partindo-se do fato que a expressão da energia interna 





Caso a entalpia figure em função de demais grandezas que não as citadas, a exemplo em função da temperatura T ou mesmo do volume V, tal expressão não constituirá uma equação fundamental para o sistema, caracterizando-se então apenas como uma equação de estado.
A tabela que se segue apresenta os passos a serem seguidos a fim de se obter a entalpia 

 |
|---|
 |
Determinar  e e  |
 |
| Eliminação de U e V fornece: |
| Entalpia H |
 |
 |
|---|
 |
Determinar  e e  |
 |
| Eliminação de P e H fornece: |
| Energia Interna U |
 |
- Exemplo
A equação fundamental para a Entalpia de um gás monoatômico ideal é, com 
Esta equação pode ser obtida a partir da equação fundamental para a energia interna 
A equação anterior pode facilmente ser reescrita a fim de tornar-se similar à encontrada em outros artigos da Wikipédia. Uma vez suprimidas constante(s) com unidade(s) definida(s) de forma a tornarem correta a análise dimensional,[7] esta apresentar-se-á como abaixo:
Variação de entalpia
A variação de entalpia (



Quanto ao sinal do 
- Reações exotérmicas:
. Há liberação de calor do sistema para a vizinhança.
- Reações endotérmicas:
. Há uma absorção de calor pelo sistema.
As variações de entalpia em reações químicas podem ser mensuradas via medida do calor absorvido ou liberado na reação, sendo o procedimento experimentalmente levado a cabo em aparelhos conhecidos como calorímetros.
É importante mencionar que as variações de entalpia absoluta 


assim, ao falar-se em variação, tanto faz falar-se da variação da entalpia-padrão ou falar-se da variação da entalpia absoluta. Fala-se pois simplesmente em variação de entalpia 
Entalpia, e entalpias
Em fundamento tem-se apenas uma entalpia, a antes definida entalpia absoluta - ou simplesmente entalpia. Contudo, dado um conjunto de situações específicas e similares, pode-se estabelecer "entalpias" também específicas ao conjunto, que não obstante carregam em seu nome a descrição da característica comum. Assim tem-se por exemplo a entalpia-padrão já discutida, a entalpia de formação, a entalpia de combustão, de vaporização, de dissolução, e quem sabe outras mais. Contudo todas[Nota 1] remontam, em essência e sem restrições, à definição inicial de entalpia absoluta - quando muito aparte alguma constante sem qualquer implicação prática - e à determinação das variações de entalpia ao longo dos processos que levam do estado inicial ao final. Assim, a "entalpia de combustão" nada mais é do que a variação de entalpia observada entre o estado inicial - neste caso definido como sendo um combustível + comburente - e o estado final - neste caso o produto da combustão, geralmente gás carbônico e água no caso da queima de hidrocarbonetos. As demais "entalpias" seguem o mesmo padrão.
Entalpia-padrão
Teoricamente, o cálculo do valor do 




Em vista da situação há pois uma liberdade de escolha quanto ao "nível" de referência ao qual associar-se-á por definição um valor de entalpia nulo visto que não há razão prática alguma que acarrete a necessidade da entalpia "zero" encontrar-se obrigatoriamente associada - como encontra-se na definição de entalpia absoluta - a um estado do sistema à temperatura de zero kelvins e cujos volume e energia interna clássicos sejam nulos - ou seja, ao estado naturalmente determinado para o qual a entalpia absoluta é nula. De forma similar ao que ocorre com a determinação de diferenças de alturas, onde o valor obtido para a espessura ("altura") de uma mesa - ou seja, a diferenças de alturas entre o topo e o pé da mesa - independe do nível de referência escolhido para medirem-se as alturas a serem subtraídas - podendo estas serem medidas tanto em relação o piso da sala como em relação o nível do mar sem contudo afetar-se o resultado de interesse prático - pode-se em princípio também escolher um nível de referência qualquer a partir do qual as entalpias serão mensuradas e a partir dos quais as variações de entalpia sejam sempre corretamente determináveis.
Embora a escolha do "nível" de referência seja em princípio livre, é extremamente valioso que este estabeleça-se um padrão experimentalmente bem definido e que seja por todos facilmente reprodutível e universalmente reconhecido, de forma a permitir a fácil determinação dos valores de entalpia para as mais variadas substâncias puras compostas visto que isso certamente facilitará muito o cálculo teórico do 

Tem-se pois que pela definição as entalpias-padrão do hidrogênio (


É conveniente explicitar-se que, conforme definidas, a entalpia absoluta e a entalpia-padrão diferem entre si por uma mera subtração de um valor adequadamente escolhido para cada situação:

Uma vez estabelecido o padrão de referência e uma forma de mensurarem-se as entalpias-padrão dos sistemas nos seus diversos estados, mostra-se também válido estabelecer alguns conceitos de utilidade prática derivados, a exemplo os conceitos de entalpias de formação e de entalpia de combustão das substâncias.
Entalpia de formação
Refere-se à energia liberada ou absorvida quando um mol de um composto se forma a partir de substâncias simples no estado padrão - as quais têm entalpia-padrão por definição igual a zero.[9]
Exemplo:
A equação acima indica que a entalpia de formação do etanol :
Entalpia de combustão
Refere-se à energia liberada na combustão de um mol de um composto; desde que todos os participantes da reação estejam no estado-padrão.
Exemplo:
A equação acima indica que a entalpia de combustão do metano :
Entalpia de ligação
Outra forma de calcular a variação de entalpia de uma reação química envolve o conceito de energias de ligação, ou seja, aquela relacionada à variação da energia potencial associada à força que une os átomos: entalpia de ligação é a energia necessária para romper um mol de ligações químicas entre pares de átomos no estado gasoso.
É importante ressaltar que a entalpia de ligação será sempre positiva visto que, pela definição, a exemplo do hidrogênio, tem-se a seguinte ordem entre reagente e produto:
e não o contrário
(incorreto) 
Considerando que a quebra de ligações é um processo endotérmico, e que a formação de ligações é um processo exotérmico, uma forma prática de calcular-se o 
Encontram-se com facilidade na literatura tabelas contendo as entalpias de ligação para as mais variadas ligações. A partir das mesmas é possível fazer-se uma estimativa das variações de entalpia em processos envolvendo reagentes e produtos definidos por tais ligações. A exemplo, pode-se determinar a variação de entalpia associada à reação (∆H=?):
uma vez conhecidos as entalpias de ligação:[12]
| C–H | +413,4 KJ/mol |
| O=O | +468,6 KJ/mol |
| C=O | +804,3 KJ/mol (para CO2) |
| H–O | +463,5 KJ/mol |
Vistos que todos os elementos encontram-se no estado gasoso, assumidos nas condições normais de temperatura e pressão, pode-se determinar a requisitada variação de entalpia, que corresponde à entalpia do estado final (produtos) menos a entalpia do estado inicial (reagentes) de duas maneiras:[13]
1) Pela diferença entre as entalpias de formação ∆H 0F (= H0F) dos produtos e dos reagentes.
2) Pela diferença entre as entalpias de ligação ∆HL (= HL) das ligações rompidas e das ligações formadas.
Como dispõe-se das entalpias de ligação, sendo este o caso em consideração, aplicar-se-á a regra 2. Tem-se assim:
a) Ligações a serem quebradas: 4 mols de ligações C-H para desfazer-se o metano, 2 mols de ligações O=O para desfazerem-se os dois mols de O2.
Tem-se que a soma das entalpias de ligação para as ligações a serem quebradas vale:

b) Ligações a serem formadas: 2 mols de ligações C=O formam 1 mol de CO2 ; 4 mols de ligações H-O formando 2 mols de H2O.
Tem-se que a soma das entalpias de ligação associadas às ligações que serão formadas vale:
A variação de entalpia para a reação inicial de combustão do metano vale, segundo a regra 2, a diferença entre as entalpias de ligação quebradas [


de onde
A reação é exotérmica visto que a variação de entalpia é negativa, conforme esperado por se tratar da combustão do metano, e libera aproximadamente 871,8 KJ de energia via calor. A entalpia do estado final é cerca de 871,8 KJ menor do que a entalpia do estado inicial.
Entendendo os cálculos
O mecanismo em questão para o cálculo de 
Em uma segunda etapa tem-se a reação:
cuja variação de entalpia é determinada pelo negativo do segundo somatório (-Σ HL(formadas)), visto que as ligações são agora formadas e não quebradas.
Trata-se assim da decomposição da reação original em duas etapas levada a cabo via inserção de um estado intermediário contendo elementos não ligados. Conforme esperado pelo fato da entalpia ser função de estado, a variação de entalpia total será a soma das variações de entalpia associadas a cada etapa da reação, o que leva corretamente, conforme esperado, a:
Entalpia de ligação ou energia de ligação?
Uma vez resolvido o problema conforme apresentado, de grande importância perceber que, embora seja verdade que para determinarem-se as ligações a serem rompidas deva-se olhar sobretudo para o lado da equação correspondente aos reagentes, e que para determinarem-se as reações a serem feitas deva-se olha prioritariamente para o lado da equação correspondente aos produtos, a primeira somatória acima (a soma das entalpias de ligação para as ligações quebradas,(Σ HL(rompidas)), não é um cálculo que fornece por resultado a entalpia HR - quer absoluta, quer padrão, quer em relação a qualquer nível pré-estabelecido - do estado inicial (dos reagentes), ou seja, esta expressão não representa o cálculo da entalpia do estado do sistema antes da reação; e que a segunda somatória em questão, (Σ HL(formadas)), não é um cálculo válido acerca da determinação da entalpia do estado final HP - quer absoluta, quer padrão, quer em relação a qualquer nível pré-estabelecido - ou seja, do estado associado aos produtos da reação, quando já formados. A equação acima, por tal, não implica que esteja-se a fazer, a fim de determinar-se a variação de entalpia ∆H na combustão do metano, “a diferença de entalpias dos reagentes e dos produtos (HR – HP)”, pois não se está a determinar, com cada parcela da mesma, a entalpia dos reagentes, HR, e dos produtos, HP. Em verdade o cálculo acima, após concluído, configura uma forma alternativa de determinar-se a variação da entalpia associada à reação, ou seja, uma forma alternativa ao método tradicional onde faz-se - por definição de variação - o valor da entalpia do estado final – dos produtos - menos a entalpia do estado inicial – dos reagentes.
Escreve-se corretamente pois que:
(correto)
e não que
(incorreto) ![\Delta H=[H_{R}]-[H_{P}]\;\;\;\;(=[\Sigma H_{{(rompidas)}}^{L}]-[\Sigma H_{{(formadas)}}^{L}])](https://wikimedia.org/api/rest_v1/media/math/render/svg/12f4197eca734805681d14a68f3c7fc4dbfbc5e5)
Poder-se-ia em princípio, contudo, a fim de evitar-se confusão certa quanto a não diferenciação explicita do "H" que figura ante e dos "H" que figuram depois do sinal de igual na sentença anterior - e eles são diferentes, o primeiro representando a entalpia do sistema e os demais entalpias de ligação - argumentar que embora a expressão anterior não encontre-se escrita de forma correta, para uma dada reação qualquer esta contudo seria valida:
(inadequado, embora "aceita" por alguns autores)
O problema com esta notação reside em um ponto bem simples: a ausência de referencial padrão teórico e experimentalmente válio para a medida da "entalpia de ligação" a ser adotado em sua definição, ou seja, na tentativa de definir-se uma nova função de estado para o sistema a ser nomeada "entalpia de ligação" 
Não há dúvidas que a entalpia de ligação e tradicional devam ser definidas de formas distintas visto que, dados o estado inicial e o estado final do sistema, o intuito é definir a entalpia de ligação de forma que um aumento em seu valor (

Em hipótese a opção para referencial seria o estado intermediário inserido no processo a fim de suportar o raciocínio sendo considerado, ou seja, seria o estado de referência um estado onde encontrar-se-iam apenas elementos isolados - desprovidos de qualquer ligação. Definir-se a “entalpia de ligação” deste estado como zero, e por conseguinte, a entalpia de ligação de um estado em particular seria definida, em acordo com a situação, como o negativo da variação de entalpia (tradicional) associada à formação de um elemento via estabelecimento de ligações entre os átomos avulsos em questão. Ter-se-ia pois a entalpia de ligação sempre positiva, e que
Ressalta-se que tal definição - que tenta ser condizente com a real definição de entalpia de ligação - seria contudo apenas complicadora, visto que o estado contendo apenas átomos sem ligação, excetuado gases nobres, é experimentalmente muito mais inacessível do que um sistema contendo elementos em estado padrão, e de forma mais inquietante, que este estado, tipicamente embora não necessariamente, implica um estado do sistema fora de seu equilíbrio termodinâmico. E para estados fora do equilíbrio não se definem os potenciais termodinâmicos, a exemplo, uma entalpia.
Grosso modo, fazê-lo seria pois apenas - a menos de um sinal - dar nova definição à “entalpia-padrão” - mediante mudança do nível de referência - de forma a apenas, em princípio, complicá-la teórica e experimentalmente.
Da forma que a entalpia de ligação é realmente definida - alguns autores mencionam apenas energia de ligação talvez por esta razão - a entalpia de ligação não é propriedade de um estado em particular e sim uma propriedade de um processo em específico onde há quebra de determinada ligação em particular, e em verdade, de forma mais detalhada - onde há a quebra de ligação entre um radical e um elemento em particular. A proposta de notação
(inadequado, embora "aceita" por alguns autores)
é por tal, inadequada: busca expressar um raciocínio válido (a lei de Hess), contudo de forma infeliz.
Confirma-se tal afirmação observando que, embora uma variação na entalpia de ligação implique realmente uma variação na entalpia-padrão do sistema, há diversos processos que implicam uma variação da entalpia-padrão do sistema sem que contudo estes impliquem uma variação na energia de ligação de seus componentes. A associação conforme feita seria, pois, de mão única.
A alternativa para expressar-se o que realmente ocorre é definir-se uma energia de ligação - a nomear-se aqui por EL de forma a nitidamente dissociar o conceito de energia de ligação do conceito de entalpia e conectá-lo ao conceito de calor de reação, e afirmar que variações na energia de ligação, quando presentes, implicam variações correspondentes na entalpia do sistema determináveis segundo a expressão:
(correto) ![\Delta E^{L}=>\Delta H=H_{P}-H_{R}=[\Sigma H_{{(rompidas)}}^{L}]-[\Sigma H_{{(formadas)}}^{L}]=[E_{R}]-[E_{P}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/47a963d6fd4be764ba0189d291e00f5ee8589c34)
Não sendo a energia de ligação promovida ao status ou uma mera re-expressão de um potencial termodinâmico do sistema, portanto.
Entalpia de dissolução
A dissolução de uma substância em água - principalmente para o caso das substâncias iônicas - ocorre sempre com transferência de energia. Uma vez verificado que a maioria das reações químicas se processa em meio aquoso, a compreensão acerca da entalpia de dissolução mostra-se importante à correta análise de tais processos.
Define-se a entalpia de dissolução como a variação de entalpia associada à dissolução de 1 mol de soluto em uma quantidade de solvente maior ou igual à mínima necessária para que se tenha a máxima variação de entalpia no processo, ou seja, para que se tenha a dissolução completa do soluto.
Um típico processo onde a entalpia de dissolução pode ser facilmente evidenciada refere-se à dissolução em água do vulgo "percloreto de ferro" - corretamente cloreto férrico - frequentemente realizada por profissionais ou amantes de eletrônica a fim de se obter uma solução adequadamente diluída de forma a poder ser utilizada no processo de corrosão de placas de circuito impresso - placas de material isolante com uma fina camada de cobre em sua superfície -, placas estas sobre as quais primeiro desenham-se e posteriormente à corrosão montam-se os circuitos eletrônicos projetados. A dissolução deve ser feita vagarosamente tamanho é o aquecimento que a mesma provoca, sempre jogando-se o percloreto na água, e nunca o contrário. A entalpia de dissolução para tal produto é consideravelmente alta em módulo - contudo negativa em valor, visto que a dissolução é exotérmica.
Dependendo do espécime químico o processo de dissolução pode em si não ser muito simples, por vezes incluindo várias etapas, as quais podem implicar respectivas variações de entalpia com sinais trocados. A exemplo, durante a dissolução de sólido iônico típico em água, em uma primeira etapa o cristal iônico é desfeito, e tal dissolução requer energia, implicando que a etapa é endotérmica (

Entalpia de vaporização
A entalpia de vaporização ou calor de vaporização é a quantidade de energia necessária para que um mol de um elemento ou de uma substância que encontre-se em equilíbrio com o seu próprio vapor passe completamente para o estado gasoso. Supõe-se a pressão constante, por padrão 1 atmosfera ou em caso contrário conforme explicitamente especificada. Mais informações, e tabela de valores para as substâncias típicas encontram-se disponíveis no artigo especialmente destinado ao assunto nesta enciclopédia eletrônica.
Entalpia de fusão
A entalpia de fusão ou calor de fusão é a quantidade de energia necessária para que um mol de um elemento ou substância em equilíbrio com seu líquido passe do estado sólido para o estado líquido mantida a pressão constante, usualmente definida como 1 atmosfera, ou conforme explicitamente especificada, em caso contrário.
Mais informações encontram-se disponíveis no artigo especialmente destinado ao assunto nesta enciclopédia eletrônica.
Processos endotérmicos, exotérmicos, e espontaneidade
O processo endotérmico é aquele que ocorre com absorção de energia na forma de calor pelo sistema. Um exemplo disso: se um pedaço de gelo for deixado sobre a mesa à temperatura ambiente, ele receberá energia na forma de calor do ambiente e isso provocará a fusão do gelo. A transição da água no estado sólido para o estado líquido é um processo em que há calor da vizinhança para o sistema, ou seja, é endotérmica.
Outro exemplo: quando um mol de óxido de mercúrio sólido se decompõe, à pressão constante, em um mol de mercúrio líquido e meio mol de oxigênio gasoso, ocorre a absorção de 90,7 kJ de energia do ambiente. Matematicamente:
Que também pode ser representada por:
O processo exotérmico é aquele que ocorre com liberação de energia na forma de calor para a vizinhança. Pode-se citar o seguinte como exemplo: quando um sistema formado por água líquida é colocado em um congelador, ele perde energia na forma de calor para esse ambiente e, em decorrência disso, ocorre a solidificação da água. Assim, transição da água no estado líquido para o estado sólido é um processo em que há calor do sistema para a vizinhança: é exotérmico.
Outro exemplo: quando um mol de hidrogênio gasoso reage, à pressão constante, com meio mol de oxigênio gasoso para formar um mol de água líquida, ocorre a liberação de 285,8 kJ de energia para o meio ambiente. Matematicamente:
Que também pode ser representada por:
Repare a correspondência entre os sinais das respectivas variações nas entalpias-padrão e a natureza da reação. Em reações exotérmicas há calor do sistema para a vizinhança, o que implica que a entalpia final do sistema é sempre menor do que a inicial; a diferença 





Relevante ao contexto é a falsa afirmação de que reações exotérmicas (

Fatores que influenciam o valor da variação de entalpia
- Quantidade de reagentes e produtos: o valor do
de uma reação varia em função da concentração de cada um de seus participantes. O aumento da concentração provoca um aumento proporcional da variação de entalpia.
Exemplo:
- Os estados físicos dos reagentes e produtos: substâncias no estado sólido provocam variações de entalpia maiores do que no estado líquido; e estas, maiores do que no estado gasoso.
Exemplo:
- Estado alotrópico de reagentes e produtos: cada estado alotrópico tem um valor de entalpia distinto.
Exemplo:
- Temperatura.
Uma reação exoenergética em uma dada temperatura pode mostrar-se endoenergética em outra temperatura, de forma que as temperaturas dos reagentes e produtos devem — quando fora do padrão — ser especificadas.
Lei de Hess
Em 1840, um físico chamado Germain Henry Hess, com base em seus estudos sobre calores de reação, descobriu que, de um modo geral, quando uma reação se dá em etapas, a soma dos calores de reação correspondentes aos diversos estágios é igual ao calor de reação obtido quando a reação é realizada completamente em uma só etapa.
Então, enunciou sua lei: "Quando uma reação química apresenta etapas intermediárias, a variação de entalpia da reação geral equivale à soma das variações de entalpia de cada uma das etapas intermediárias". A lei de Hess implica a verificação experimental de que a entalpia é uma função de estado, ou seja, de que a variação da entalpia depende em um sistema depende apenas dos estados inicial e final do sistema - sendo sempre determinável pela diferença 
Podemos utilizar como exemplo simples da aplicação da Lei de Hess a reação de oxidação do carbono. É possível que o carbono se combine com um único átomo de oxigênio, formando o monóxido de carbono:
O monóxido de carbono é combustível, isto é, ele pode se combinar com outro átomo de oxigênio, produzindo dióxido de carbono; por este motivo, ocorre a reação de combustão:
Se somarmos estas duas equações (como se elas fossem equações algébricas), poderíamos também, segundo a Lei de Hess, somar as entalpias de reação:
Continuando a utilizar regras análogas às empregadas na álgebra, podemos eliminar todos os elementos que aparecem nos dois membros da equação - neste caso, eliminamos o 
Somando 

que é exatamente a entalpia da reação se queimássemos diretamente o carbono a dióxido de carbono.
em um dado processo termodinâmico - ou seja, a diferença entre as entalpias do estado final 

- Gerar link
- X
- Outros aplicativos









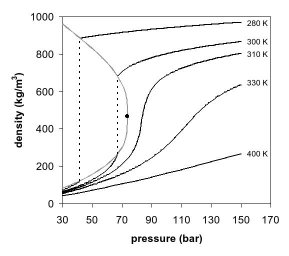



















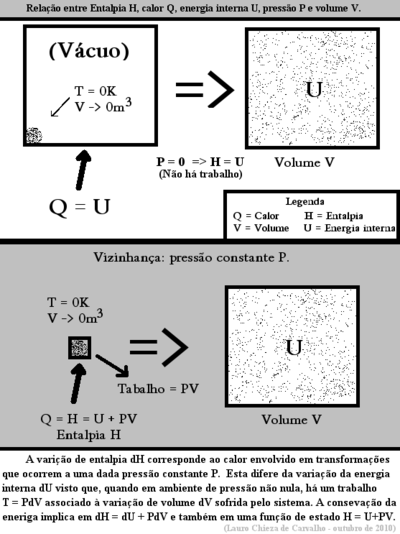





![H(S,P,N)={\frac {5}{2}}Nk\left(P\Phi \,e^{{[({\frac {S}{Nk}}-c)-{\frac {5}{2}}]}}\right)^{{{\frac {2}{5}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9804bb5921b121117cc9af3a325e91b827da7a3)

![U_{{(S,V,N)}}=N({\frac {N}{V}})^{{{\frac {2}{3}}}}e^{{[{\frac {2}{3}}({\frac {S}{Nk_{B}}}-c)]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12cc8927c7289a257629d531b8232a6007cb92c7)












![\Delta H=[H_{R}^{L}]-[H_{P}^{L}]=-\Delta H^{L}\;\;\;\;(=[\Sigma H_{{(rompidas)}}^{L}]-[\Sigma H_{{(formadas)}}^{L}])](https://wikimedia.org/api/rest_v1/media/math/render/svg/433c00ff33e3c96033edba97961691a3fd79820e)
















Comentários
Postar um comentário