O MUNDO DAS DIMENSÕES DE GRACELI
- Gerar link
- X
- Outros aplicativos
O MUNDO DAS DIMENSÕES DE GRACELI.
ONDE NÃO APENAS O ESPAÇO E O TEMPO SÃO SÃO DIMENSÕES, MAS TAMBÉM TODA FORMA DE ESTRUTURAS, ENERGIAS, CATEGORIAS, FENÔMENOS E ESTADOS FÍSICOS E QUÂNTICO E ESTADOS DE GRACELI. CONFIGURAÇÃO ELETRÔNICA , E OUTTOS
ONDE FORMAM O INFINITO-DIMENSIONAL DE GRACELI.
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.
ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.
NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.
JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.
TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :
sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
sistema indeterminístico Graceli ;
SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +
SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos
SISTEMA GRACELI INFINITO-DIMENSIONAL.
SISTEMA GRACELI INFINITO-DIMENSIONAL.
COM ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.
ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.
TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO E ESPECÍFICO NÍVEL DE ENERGIA.
SISTEMA MULTIDIMENSIONAL GRACELI
ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.
Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].
Em física, termodinâmica, química, físico-química e física da matéria condensada, um ponto crítico, também chamado de estado crítico, ocorre sob condições (tais como valores específicos de temperatura, pressão ou composição) no qual não existem limites de fase. Existem vários tipos de pontos críticos, incluindo pontos críticos líquido-vapor e líquido-líquido.[1][2]
Substâncias puras: ponto crítico líquido-vapor
O "ponto crítico" é por vezes usado para denotar o ponto especificamente vapor-líquido crítico de um material, a partir do qual a distinção entre fase a líquida e gasosa não existe.
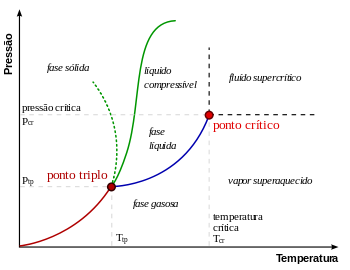
O ponto crítico de vapor-líquido em um diagrama de fases pressão-temperatura está no extremo de alta temperatura do limite de fase líquido-gás. A linha pontilhada verde mostra o comportamento anômalo da água.[3]
Como se mostra no diagrama de fases para a direita, isto é o ponto em que a fronteira entre a fase líquida e gasosa termina. Em água, o ponto crítico ocorre em cerca de 647 K. (374 ° C; 705 ° F) e 22,064 MPa (218 atm)
À medida que a substância se aproxima da temperatura crítica, as propriedades da sua fases gasosa e líquida convergem, resultando em apenas uma fase no ponto crítico: um fluido supercrítico homogêneo. O calor de vaporização é zero no ponto crítico e para além dele, por isso não existe distinção entre as duas fases. No diagrama de Pressão-temperatura, o ponto em que a temperatura crítica e pressão crítica satisfazer é chamado de ponto crítico da substância. Acima da temperatura crítica, um líquido não pode ser formada por um aumento da pressão, apesar de um sólido poder ser formado sob uma pressão suficiente. A pressão crítica é a pressão de vapor, à temperatura crítica. O volume crítico é o volume molar de uma mole do material a uma temperatura e pressão críticas.
Propriedades críticas variam de material para material, e para muitas substâncias puras estão prontamente disponíveis na literatura. No entanto, a obtenção de propriedades críticas para misturas é mais desafiador.
Definição matemática
No caso das substâncias puras, há um ponto de inflexão na curva isotérmica crítica (linha de temperatura constante) com um diagrama de Pressão-Volume. Isto significa que, no ponto crítico: [4][5][6]
- //////
- O MUNDO DAS DIMENSÕES DE GRACELI.
Isto é, as primeira e segunda derivadas parciais da pressão p no que diz respeito ao volume V são ambos zero, com as derivadas parciais avaliados em temperatura constante T. Esta relação pode ser usada para avaliar dois parâmetros de uma equação de estado em termos das propriedades críticas, tais como os parâmetros a e b na equação de van der Waals.[4]
Às vezes um conjunto de propriedades reduzidas é definida em termos das propriedades importantes, isto é:[7]
- //////
- O MUNDO DAS DIMENSÕES DE GRACELI.
- //////
- O MUNDO DAS DIMENSÕES DE GRACELI.
- //////
- O MUNDO DAS DIMENSÕES DE GRACELI.
- //////
- O MUNDO DAS DIMENSÕES DE GRACELI.
- //////
- O MUNDO DAS DIMENSÕES DE GRACELI.
- //////
- O MUNDO DAS DIMENSÕES DE GRACELI.
onde 



História
A existência de um ponto crítico foi descoberto pela primeira vez por Charles Cagniard de la Tour em 1822[8] [9] e nomeado por Thomas Andrews, em 1869.[10] Ele mostrou que o CO2 poderia ser liquefeito a 31 ° C a uma pressão de 73 atm, mas não a uma temperatura ligeiramente mais elevada, mesmo sob uma pressão muito mais elevada (até 3,000 atm).
Misturas: ponto crítico líquido-líquido
O ponto crítico líquido-líquido de uma solução, o que ocorre a uma temperatura crítica da solução, ocorre no limite da região de duas fases no diagrama de fases. Em outras palavras, é o ponto no qual uma mudança infinitesimal em alguma variável termodinâmica (tais como a temperatura ou a pressão), conduzirá a separação da mistura em duas fases líquidas distintas, como se mostra no diagrama de fases do polímero-solvente à direita. Existem dois tipos de pontos críticos líquido-líquido, que são a temperatura de solução crítica superior , em inglês (UCST), representa o ponto mais quente na qual o arrefecimento irá induzir a separação de fases, e a temperatura de solução crítica inferior, em inglês (TCIS), que é o ponto mais frio no qual o aquecimento irá induzir a separação de fases.
Definição matemática
Do ponto de vista teórico, o ponto crítico líquido-líquido representa o extremo da temperatura da concentração da curva spinodal (como pode ser visto na figura, à direita). Assim, o ponto crítico líquido-líquido em um sistema de dois componentes deve satisfazer duas condições: condição da curva spinodal (a segunda derivada da energia livre em relação a concentração deve ser igual a zero), e da condição extrema (a terceira derivada da energia livre no que diz respeito à concentração também deve ser igual a zero ou a derivada da temperatura spinodal com respeito à concentração deve ser igual a zero).
O ponto de fusão designa a temperatura à qual uma substância passa do estado sólido ao estado líquido. Eis abaixo uma breve lista dos elementos químicos e seus respectivos pontos de fusão.
Elementos químicos em ordem crescente do ponto de fusão
| Elemento | Símbolo | Número atômico (Z) | Ponto de fusão (K) | Ponto de fusão (°C) |
| Hélio | He | 2 | 0,95 | -272,2 |
| Hidrogênio | H | 1 | 13,81 | -259,34 |
| Neônio | Ne | 10 | 24,56 | -248,59 |
| Flúor | F | 9 | 53,53 | -219,52 |
| Oxigênio | O | 8 | 54,85 | -218,3 |
| Nitrogênio | N | 7 | 63,25 | -209,9 |
| Argônio | Ar | 18 | 83,8 | -189,35 |
| Criptônio | Kr | 36 | 115,77 | -157,38 |
| Xenônio | Xe | 54 | 161,36 | -117,79 |
| Cloro | Cl | 17 | 171,65 | -101,5 |
| Radônio | Rn | 86 | 202,15 | -71,8 |
| Fleróvio | Fl | 114 | 210 (estimado) | -63,15 |
| Mercúrio | Hg | 80 | 234,32 | -38,83 |
| Bromo | Br | 35 | 265,95 | -7,2 |
| Frâncio | Fr | 87 | 300,15 | 27 |
| Césio | Cs | 55 | 301,65 | 28,5 |
| Gálio | Ga | 31 | 302,91 | 29,76 |
| Rubídio | Rb | 37 | 312,46 | 39,31 |
| Fósforo | P | 15 | 317,35 | 44,2 |
| Oganésson | Og | 118 | 320 (estimado) | 46,85 |
| Potássio | K | 19 | 336,65 | 63,5 |
| Sódio | Na | 11 | 370,95 | 97,8 |
| Iodo | I | 53 | 386,85 | 113,7 |
| Enxofre | S | 16 | 392,75 | 115,21 |
| Índio | In | 49 | 429,75 | 156,6 |
| Lítio | Li | 3 | 453,65 | 180,5 |
| Selênio | Se | 34 | 493,65 | 220,5 |
| Estanho | Sn | 50 | 505,08 | 231,93 |
| Polônio | Po | 84 | 527,15 | 254 |
| Bismuto | Bi | 83 | 544,45 | 271,3 |
| Astato | At | 85 | 575,15 | 302 |
| Tálio | Tl | 81 | 577,15 | 304 |
| Cádmio | Cd | 48 | 594,22 | 321,07 |
| Chumbo | Pb | 82 | 600,61 | 327,46 |
| Moscóvio | Mc | 115 | 670 (estimado) | 396,85 |
| Zinco | Zn | 30 | 692,73 | 419,58 |
| Nipônio | Nh | 113 | 700 (estimado) | 426,85 |
| Telúrio | Te | 52 | 722,66 | 449,51 |
| Antimônio | Sb | 51 | 903,78 | 630,63 |
| Netúnio | Np | 93 | 910,15 | 637 |
| Plutônio | Pu | 94 | 912,55 | 639,4 |
| Magnésio | Mg | 12 | 923,15 | 650 |
| Alumínio | Al | 13 | 933,15 | 660 |
| Rádio | Ra | 88 | 973,15 | 700 |
| Bário | Ba | 56 | 1 000,15 | 727 |
| Estrôncio | Sr | 38 | 1 050,15 | 777 |
| Cério | Ce | 58 | 1 071,15 | 798 |
| Arsênio | As | 33 | 1 090,15 | 817 |
| Európio | Eu | 63 | 1 095,15 | 822 |
| Itérbio | Yb | 70 | 1 097,15 | 824 |
| Mendelévio | Md | 101 | 1 100,15 | 827 |
| Nobélio | No | 102 | 1 100,15 | 827 |
| Cálcio | Ca | 20 | 1 115,15 | 842 |
| Einstênio | Es | 99 | 1 133,15 | 860 |
| Califórnio | Cf | 98 | 1 173,15 | 900 |
| Lantânio | La | 57 | 1 193,15 | 920 |
| Praseodímio | Pr | 59 | 1 203,95 | 930,8 |
| Germânio | Ge | 32 | 1 211,45 | 938,3 |
| Prata | Ag | 47 | 1 234,93 | 961,78 |
| Berquélio | Bk | 97 | 1 259,15 | 986 |
| Neodímio | Nd | 60 | 1 294,15 | 1 021 |
| Actínio | Ac | 89 | 1 323,15 | 1 050 |
| Ouro | Au | 79 | 1 337,33 | 1 064,18 |
| Cobre | Cu | 29 | 1 357,77 | 1 084,62 |
| Promécio | Pm | 61 | 1 373,15 | 1 100 |
| Urânio | U | 92 | 1405,35 | 1 132,2 |
| Amerício | Am | 95 | 1 449,15 | 1 176 |
| Manganês | Mn | 25 | 1 519,15 | 1 246 |
| Berílio | Be | 4 | 1 560,15 | 1 287 |
| Gadolínio | Gd | 64 | 1 586,15 | 1 313 |
| Cúrio | Cm | 96 | 1 613,15 | 1 340 |
| Térbio | Tb | 65 | 1 629,15 | 1 356 |
| Disprósio | Dy | 66 | 1 685,15 | 1 412 |
| Silício | Si | 14 | 1 687,15 | 1 414 |
| Níquel | Ni | 28 | 1 728,15 | 1 455 |
| Hólmio | Ho | 67 | 1 743,15 | 1 470 |
| Cobalto | Co | 27 | 1 768,15 | 1 495 |
| Ítrio | Y | 39 | 1 795,15 | 1 522 |
| Férmio | Fm | 100 | 1 800,15 | 1 527 |
| Érbio | Er | 68 | 1 802,15 | 1529 |
| Ferro | Fe | 26 | 1 811,15 | 1 538 |
| Escândio | Sc | 21 | 1 814,15 | 1 541 |
| Túlio | Tm | 69 | 1 818,15 | 1 545 |
| Paládio | Pd | 46 | 1 827,15 | 1 554 |
| Protactínio | Pa | 91 | 1 845,15 | 1 572 |
| Laurêncio | Lr | 103 | 1 900,15 | 1 627 |
| Lutécio | Lu | 71 | 1 936,15 | 1 663 |
| Titânio | Ti | 22 | 1 941,15 | 1 668 |
| Samário | Sm | 62 | 1 977,15 | 1 704 |
| Tório | Th | 90 | 2 023,15 | 1 750 |
| Platina | Pt | 78 | 2 041,55 | 1 768,4 |
| Zircônio | Zr | 40 | 2 128,15 | 1 855 |
| Crômio | Cr | 24 | 2 180,15 | 1 907 |
| Vanádio | V | 23 | 2 183,15 | 1 910 |
| Ródio | Rh | 45 | 2 237,15 | 1 964 |
| Boro | B | 5 | 2 348,15 | 2 075 |
| Rutherfórdio | Rf | 104 | 2 400 (estimado) | 2 126,85 |
| Tecnécio | Tc | 43 | 2 430,15 | 2 157 |
| Háfnio | Hf | 72 | 2 506,15 | 2 233 |
| Rutênio | Ru | 44 | 2 607,15 | 2 334 |
| Irídio | Ir | 77 | 2 719,15 | 2 446 |
| Nióbio | Nb | 41 | 2 750,15 | 2 477 |
| Molibdênio | Mo | 42 | 2 896,15 | 2 623 |
| Tântalo | Ta | 73 | 3 290,15 | 3 017 |
| Ósmio | Os | 76 | 3 306,15 | 3 033 |
| Rênio | Re | 75 | 3 459,15 | 3 186 |
| Tungstênio | W | 74 | 3 695,15 | 3 414 |
| Carbono | C | 6 | 3 800,15 | 3 527 |
| Bóhrio | Bh | 107 | – | – |
| Copernício | Cn | 112 | – | – |
| Darmstádtio | Ds | 110 | – | – |
| Dúbnio | Db | 105 | – | – |
| Hássio | Hs | 108 | – | – |
| Livermório | Lv | 116 | – | – |
| Meitnério | Mt | 109 | – | – |
| Roentgênio | Rg | 111 | – | – |
| Seabórgio | Sg | 106 | – | – |
| Tenesso | Ts | 117 | – | – |
Todos os fenômenos físicos que ocorrem na natureza podem ser descritos em termos de quatro interações fundamentais. Elas são fundamentais no sentido de que não podem ser reduzidas a interações mais básicas. Cada interação descreve como uma dada característica, como a massa de uma partícula, ou conjunto de partículas, afeta outras partículas com essa mesma característica.
Segundo o modelo padrão, cada uma dessas interações é mediada pela troca de bósons entre as partículas na qual elas atuam. Essas partículas que mediam as interações são virtuais e, por isso, não podem ser observadas diretamente. Isso justifica o porquê de os efeitos dessas interações não serem sentidas instantaneamente, já que a maior velocidade que elas podem se propagar é com a velocidade da luz. Para que uma partícula virtual possa ser emitida sem violar a conservação de energia, a mesma deve ser reabsorvida em um intervalo de tempo tão curto quanto o permitido pelo princípio da incerteza. Porém, esses bósons mediadores podem ser tornar reais caso seja fornecida energia equivalente à energia de repouso deles.[2]
Consequentemente o alcance de uma dada interação está relacionado com a massa do bóson mediador. Assim, quanto maior a massa do bóson mediador, menor será o alcance da interação. Cada interação também apresenta um chamado tempo de interação, de forma que a troca de bósons virtuais é feita dentro desse tempo.
A intensidade de cada interação é definida pela sua constante de acoplamento, um parâmetro adimensional que serve para comparar as diferentes interações. No caso particular da interação eletromagnética, a constante de acoplamento é obtida a partir da expressão da energia potencial eletrostática entre duas cargas puntiformes divida pelor fator ħc.
A constante de acoplamento da interação eletromagnética é também conhecida como a constante de estrutura fina 
| Interação | Bóson mediador | Massa ( ) ) | Fonte | Alcance (m) | Tempo de interação (s) | Constante de acoplamento |
|---|---|---|---|---|---|---|
| Forte | Glúon | 0 | Carga de cor |  |  |  |
| Eletromagnética | Fóton | 0 | Carga elétrica |  |  |  |
| Fraca |  | 81,91 | Carga fraca |  |  |  |
| Gravitacional | Gráviton | 0 | Massa |  |  |  |
Em termodinâmica, o ponto triplo é um estado particular de uma substância determinado por valores de temperatura e pressão, no qual as três fases ou estados físicos da substância (sólido, líquido e gasoso) coexistem em equilíbrio.[1]
O ponto triplo do dióxido de carbono (CO2), por exemplo, ocorre na temperatura de 216,55 K e à pressão de 517 kPa. Já o ponto triplo do mercúrio ocorre à temperatura de −38,83440 °C e à pressão de 0,2 mPa.
Além do ponto triplo entre sólido, líquido e gasoso, podem existir pontos triplos envolvendo mais de uma fase sólida, nas substâncias com polimorfismo. Em geral, para um sistema com p fases possíveis, existem 
pontos triplos.[1]
Note que a pressão aqui referida é a pressão de vapor da substância — não a pressão total do sistema.
O ponto triplo da água é dado por definição - não por uma medição exata. É usado para definir o kelvin, a unidade de temperatura termodinâmica no Sistema Internacional de Unidades.[2][3] Os pontos triplos de várias substâncias são usados para definir pontos na Escala Internacional de Temperaturas de 1990 (ITS-90), que vai desde o ponto triplo do hidrogênio (13,8033 K) até o ponto triplo da água (273,16 K, 0,01 °C ou 32,018 °F)
Pontos triplos da água
Ponto triplo sólido-líquido-gás
A única combinação de pressão e temperatura na qual os três estados físicos da água (sólido (gelo), gasoso (vapor) e líquido) podem coexistir em equilíbrio estável ocorre exatamente quando a temperatura é de 273,16 kelvins (0,01 °C) e a pressão é de 611,73 pascals (cerca de 0,006 bar; 0,0060373 atm). Nesse ponto, é possível mudar toda a substância para gelo, água ou vapor fazendo pequenas mudanças na temperatura e pressão.
O ponto triplo sólido-líquido-gás corresponde à mínima pressão na qual a água líquida pode existir. Sob pressões abaixo do ponto triplo (como no espaço sideral), o gelo, quando aquecido a uma pressão constante, converte-se diretamente em vapor de água, num processo conhecido como sublimação. Acima do ponto triplo, o gelo, quando aquecido a uma pressão constante, primeiro derrete, formando água líquida, e depois evapora ou ferve, passando ao estado gasoso (vapor).
Para a maioria das substâncias, o ponto triplo também é a mínima temperatura na qual o líquido pode existir. Para a água, porém, isto não é verdade, por causa de seu comportamento anômalo[4] que faz com que o ponto de fusão do gelo diminua com o aumento da pressão, conforme mostra a linha verde pontilhada, no diagrama de fases (ver figura). A uma temperatura um pouco abaixo do ponto triplo (entre 251–273 K), a compressão a temperatura constante transforma o vapor de água, primeiro, em gelo I e depois em água líquida (o gelo tem uma densidade menor do que a água líquida, de modo que um aumento de pressão leva à liquefação).
Durante a missão Mariner 9, da NASA, para Marte, a pressão do ponto triplo da água foi usada como ponto de referência para o "nível do mar". Missões mais recentes utilizam altimetria a laser e medições da gravidade, em vez da pressão, para definir elevações em Marte.[5]
Outros pontos triplos da água em pressões mais altas
Em altas temperaturas, a água tem um diagrama de fases complexo com quinze fases conhecidas do gelo e um número de pontos triplos, incluíndo os dez cujas coordenadas são mostradas no diagrama. Por exemplo, o ponto triplo em 251 K (-22 °C) e 210 MPa (2070 atm) corresponde às condições de coexistência do gelo Ih (gelo comum), gelo III e água líquida, todos em equilíbrio. Mas podem existir também pontos em que três fases sólidas coexistam em equilíbrio, como a 218 K e 620 MPa.
Células do ponto triplo
Células do ponto triplo são usadas na calibração de termômetros. Para medições exatas, células de ponto triplo são geralmente preenchidas com uma substância química com alta pureza, como o hidrogênio, argônio, mercúrio ou água, dependendo da temperatura desejada. A pureza destas substâncias pode ser tal que apenas uma parte em um milhão seja um contaminante, o que significa 99,9999% puro. As células de ponto triplo são tão eficientes no alcance de temperaturas precisas e reproduzíveis que um padrão internacional de calibração de termômetros chamado ITS-90 se baseia em células de hidrogênio, neon, oxigênio, argônio, mercúrio e água para determinar seus seis pontos definidos de temperatura.
Tabela de pontos triplos
Esta tabela lista o ponto triplo sólido-líquido-gasoso de substâncias comuns. A menos que diferentemente indicadas, as informações vieram da U.S. National Bureau of Standars (agora NIST (National Institute of Standards and Technology).[6]
| Substância | T [K] | p [kPa]* |
|---|---|---|
| Acetileno | 192,4 | 120 |
| Amoníaco | 195,40 | 6,076 |
| Argônio | 83,81 | 68,9 |
| Arsênio | 1090 | 3628 |
| Butano | 134,6 | 7 × 10−4 |
| Carbono (grafite) | 4765 | 10132 |
| Dióxido de carbono | 216,55 | 517 |
| Monóxido de carbono | 68,10 | 15,37 |
| Clorofórmio | 175,43 | 0,870 |
| Deuterio | 18,63 | 17,1 |
| Etano | 89,89 | 8 × 10−4 |
| Etanol | 150 | 4,3 × 10−7 |
| Etileno | 104,0 | 0,12 |
| Ácido fórmico | 281,40 | 2,2 |
| Hélio-4 (ponto lambda) | 2,19 | 5,1 |
| Hexafluoroetano | 173,08 | 26,60 |
| Hidrogênio | 13,84 | 7,04 |
| Cloreto de Hidrogênio | 158,96 | 13,9 |
| Iodo[7] | 386,65 | 12,07 |
| Isobutano[8] | 113,55 | 1,9481 × 10−5 |
| Mercúrio | 234,2 | 1,65 × 10−7 |
| Metano | 90,68 | 11,7 |
| Neon | 24,57 | 43,2 |
| Óxido nítrico | 109,50 | 21,92 |
| Nitrogênio | 63,18 | 12,6 |
| Óxido nitroso | 182,34 | 87,85 |
| Oxigênio | 54,36 | 0,152 |
| Paládio | 1825 | 3,5 × 10−3 |
| Platina | 2045 | 2,0 × 10−4 |
| Dióxido de enxofre | 197,69 | 1,67 |
| Titânio | 1941 | 5,3 × 10−3 |
| Hexafluoreto de urânio | 337,17 | 151,7 |
| Água | 273,16 | 0,6117 |
| Xenônio | 161,3 | 81,5 |
| Zinco | 692,65 | 0,065 |
* Nota: Para fins de comparação, a pressão atmosférica típica é 101,325 kPa (1 atm).

Na física e na ciência dos materiais, a Temperatura de Curie (Tc), ou a temperatura no Ponto de Curie, é a temperatura na qual o magnetismo permanente de um material se torna um magnetismo induzido. A força do magnetismo é determinada pelo momento magnético.
A temperatura de Curie é o ponto crítico onde o momento magnético intrínseco do material muda de direção. Momentos magnéticos são momentos de dipolo permanentes que dentro do átomo são criados a partir do momento angular e do spin dos elétrons. Materiais tem diferentes estruturas de momentos magnéticos intrínsecos que variam com a mudança de temperatura.
Magnetismo permanente é causado pelo alinhamento dos momentos magnéticos e magnetismo induzido é criado quando momentos magnéticos desordenados são forçados a se alinhar em um campo magnético requerido. Por exemplo, os momentos magnéticos ordenados (ferromagnético, Figura 1) mudam e se tornam desordenados (paramagnético, Figura 2) na Temperatura de Curie.
Altas temperaturas fazem a magnetização espontânea de imãs mais fracos ocorrer apenas na Temperatura de Curie. Susceptibilidade magnética só ocorre acima da Temperatura de Curie e pode ser calculada pela Lei de Curie-Weiss que é derivada da Lei de Curie.
Em analogia aos materiais ferromagnéticos e paramagnéticos, a temperatura de Curie pode ser usada para descrever a temperatura onde polarização eletrostática espontânea do material se torna um polarização eletrostática induzida ou o contrário caso a temperatura seja reduzida abaixo da Temperatura de Curie.
A Temperatura de Curie recebeu esse nome depois que Pierre Curie mostrou que o magnetismo se perde depois de alcançar uma temperatura crítica.[1]
| Material | Temperatura de Curie (°C) |
|---|---|
| Ferro (Fe) | 770 |
| Cobalto (Co) | 1127 |
| Níquel (Ni) | 354 |
| Gadolínio (Gd) | 19 |
| Disprósio (Dy) | -185 |
| MnBi | 357 |
| MnSb | 314 |
| CrO2 | 113 |
| MnAs | 45 |
| EuO | -204 |
| Óxido férrico (Fe2O3) | 675 |
| Óxido de ferro(II,III) (FeOFe2O3) | 585 |
| NiOFe2O3 | 585 |
| CuOFe2O3 | 455 |
| MgOFe2O3 | 440 |
| MnOFe2O3 | 300 |
| Y3Fe5O12 | 287 |
| Ímã de neodímio | 310-400 |
| Alnico | 700-860 |
| Imã Samário-Cobre | 720-800 |
| Ferrite | 450 |
Índice
Lei de Curie-Weiss
A Lei de Curie-Weiss é uma versão
adaptada da Lei de Curie.
A Lei de Curie-Weiss é um modelo simples derivado da aproximação do campo médio, isso significa que funciona bem quando a temperatura do material,T, é muito maior que sua correspondente Temperatura de Curie,Tc, logo T >> Tc; Entretanto falha para descrever a susceptibilidade magnética, χ, na proximidade imediata do ponto de Curie por causa das flutuações locais entre os átomos.[5]
Ambas Lei de Curie e Lei de Curie-Weiss não servem quando T< Tc.
Lei de Curie para material paramagnético:[6]
- //////
- O MUNDO DAS DIMENSÕES DE GRACELI.
| Definition | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| χ | a susceptibilidade magnética; influência de um campo magnético requerido no material | |||||||||||||||||||||||||||||||||||||||||||||||||||
| M | momento magnético por unidade de volume | |||||||||||||||||||||||||||||||||||||||||||||||||||
| H | o campo magnético macroscópico | |||||||||||||||||||||||||||||||||||||||||||||||||||
| B | o campo magnético | |||||||||||||||||||||||||||||||||||||||||||||||||||
| C | a Constante Curie específica do material Em física, o momento magnético ou momento de dipolo magnético de um elemento pontual é um vetor que, em presença de um campo magnético (inerentemente vectorial), relaciona-se com o torque de alineação de ambos vectores no ponto no qual se situa o elemento . O vector de campo magnético a utilizar-se é o B denominado como Indução Magnética ou Densidade de Fluxo Magnético cuja magnitude é o Weber por metro quadrado. Em física, astronomia, química e engenharia elétrica, o termo momento magnético de um sistema (tal como um laço de corrente elétrica, uma barra de magneto, um eletrão, uma molécula, ou um planeta) normalmente refere-se a seu momento dipolo magnético, e é uma medida da intensidade da fonte magnética. Especificamente, o momento dipolo magnético quantifica a contribuição do magnetismo interno do sistema ao campo magnético dipolar externo produzido pelo sistema (i.e. o componente do campo magnético externo que atua ao inverso da distância ao cubo). Qualquer campo magnético dipolar é simétrico no que diz respeito às rotações em torno de um eixo particular, conseqüentemente é habitual descrever o momento de dipolo magnético que cria um campo como um vector com uma direção ao longo deste eixo. Para quadripolar, octopolar, e momentos magnéticos multipolos de mais alta ordem (ver expansão multipolo). Relações físicasA relação é: Onde Um dos exemplos mais simples de momento magnético é o de uma espiral condutora da electricidade, com intensidade I e área A, para a qual a magnitude é: ExemploA força resultante sobre uma bússola produzida pelo campo magnético da Terra, é quase nula, devido a que sobre os dois pólos magnéticos atuam forças iguais e opostas. No entanto, essas forças produzem um torque suficientemente forte para poder ser observado facilmente.[1] Qualquer ímã, em particular a bússola, tem um momento magnético, o torque será sempre no sentido que faz rodar o momento magnético O torque produzido pelo campo magnético é o princípio usado nos motores elétricos (figura ao lado). O motor tem uma bobina, que pode rodar à volta de um eixo, dentro de um campo magnético produzido por ímanes fixos. A bobina é um fio condutor enrolado várias vezes. Cada volta completa do fio na bobina designa-se de espira.[1] Quando o fio é percorrido por uma corrente onde O momento magnético de uma bobina é a soma dos momentos das espiras que formam essa bobina. Se a bobina tiver Se o campo não for uniforme, a área da bobina deverá ser dividida em pequenos pedaços para calcular o torque total por meio de um integral de superfície.[1] Num motor, os dois terminais da bobina ligam-se a um comutador que roda juntamente com a bobina. Na figura do motor pode ver-se o comutador (cilindro com dois setores metálicos independentes) a fazer contato com os dois terminais Quando a bobina roda, chega até uma posição em que o segmento do comutador que estava em contato com o terminal positivo passa a estar em contato com o terminal negativo e vice-versa, invertendo-se o sentido da corrente na bobina. O comutador é colocado de forma a que, quando o momento magnético da bobina estiver na direção e sentido do campo magnético do íman (de esquerda para direita, na figura do motor, o sentido da corrente seja invertido, fazendo com que o ângulo entre o momento magnético e o campo passe de Assim, a bobina roda constantemente, porque o torque magnético tende sempre a diminuir esse ângulo até Momento magnético de spinOs electrões e muitos núcleos atómicos também têm momentos magnéticos intrínsecos, cuja explicação requer tratamento mecânico quântico e que se relaciona com o momento angular das partículas. São estes momentos magnéticos intrínsecos os que dão lugar a efeitos macroscópicos de magnetismo, e a outros fenómenos como a ressonância magnética nuclear. O momento magnético de spin é uma propriedade intrínseca ou fundamental das partículas, como a massa ou a carga eléctrica. Este momento está relacionado com o fato de que as partículas elementares têm momento angular intrínseco ou spin, para partículas carregadas isso leva inevitavelmente a que se comportem de modo similar a um pequeno circuito com cargas em movimento. Entretanto, também existem partículas neutras como o neutrão que, embora tenham momento magnético, não apresentam carga (de fato o neutrão não é considerado realmente elementar senão formado por três quarks carregados).
Momento magnético do eletrãoO momento (dipolar) magnético de um eletrão é: onde
Experimento de Stern-Gerlach: A Descoberta do Momento MagnéticoEm 1943, o Prêmio Nobel de Física foi concedido ao físico alemão Otto Stern (1888- 1969) por seus trabalhos pioneiros sobre o método do feixe atômico e a conseqüente descoberta do momento magnético do próton.[3] As primeiras experiências com feixes atômicos foram realizadas por Stern e seu colega, o físico alemão Walther Gerlach (1899-1979), nas quais foi possível medir o momento magnético de átomos, fazendo passar um feixe de átomos de prata (Ag) por uma região de campo magnético não uniforme Assim, os átomos que tinham o momento magnético Através do afastamento entre as marcas deixadas pelos átomos de Ag em uma placa situada em uma das extremidades do equipamento que gerava O resultado dessas experiências, conhecido como a experiência de Stern-Gerlach, foi publicado, em 1921, na Zeitscrhift Für Physik, em 1922, também na Zeitscrhift Für Physik e, em 1924, nos Annalen der Physik. Em 1933, Stern e o físico alemão Immanuel Estermann apresentaram na Zeitscrhift Für Physik 85 (p. 17) o resultado de uma experiência, na qual mediram o momento magnético do próton, usando a mesma técnica do desvio de um feixe molecular por campos magnéticos variáveis Em 1949, Gardner e Edward Mills Purcell apresentaram, na Physical Review, o resultado de uma experiência na qual determinaram o momento magnético (µ) do Próton. Momento magnético orbitalCertas disposições orbitais, com degeneração tripla ou superior, implicam um momento magnético adicional, pelo movimento dos electrões como partículas carregadas. A situação é análoga à da espiral condutora apresentada aciba, mas exige um tratamento quântico. Os compostos dos diferentes metais de transição apresentam muitos momentos magnéticos diversos, mas é possível encontrar um intervalo típico para cada metal em cada estado de oxidação, tendo em conta, entretanto, se é de spin alto ou baixo.
O magnetão de Bohr, referido em alguns textos como magneton de Bohr, (símbolo onde:
No sistema internacional de unidades se valor é aproximadamente: No sistema CGS de unidades seu valor é aproximadamente: |
- Gerar link
- X
- Outros aplicativos







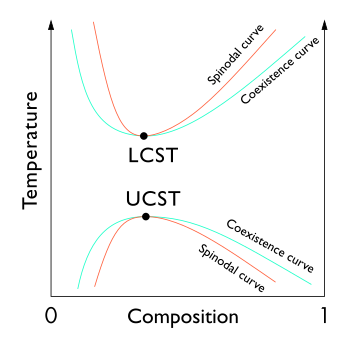








































Comentários
Postar um comentário